Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 13
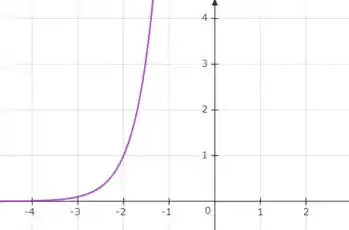
Faça um esboço do gráfico da função. Não use a calculadora. Use apenas os gráficos dados nas Figuras 3 e 13 e, se necessário, as transformações da Seção 1.3
Passo 1
Fala aí, pessoal. Tudo certinho com vocês?
Bom, essa questão pede para que a gente use os gráficos da figura 3 e da figura 13 do livro, Fazendo as transformações que forem necessárias, para esboçar o gráfico da função
Então precisaremos entender que gráficos são esses, como eles se parecem com a nossa função, e quais transformações devemos fazer para obter o gráfico que queremos.
Vem que te mostro como vamos fazer tudo isso.
Passo 2
Primeiro vamos ver qual é a figura 3 e a figura 13. Do livro, temos:
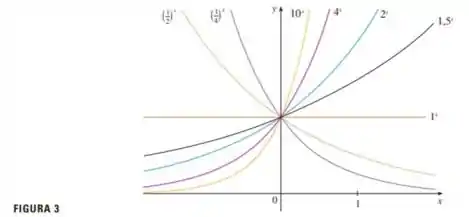
E
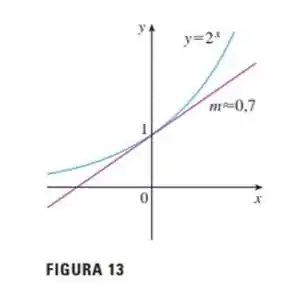
Bom pessoal, como nossa função é
O gráfico mais próximo é o que está em amarelo na figura 3. Nela podemos ver como o gráfico da função pode ser esboçado, pois ela é a função
Repare em algumas características importantes. Essa função corta o eixo em , e se aproxima do eixo , mas não o atravessa, quando os valores de tendem para .
Porém, a função no nosso exercício não é exatamente igual a esta. Temos o no expoente da função adicionado de 2 unidade. Isso indica que precisamos de uma transformação.
Passo 3
Na seção 1.3, aprendemos que quando temos uma função do tipo devemos fazer um deslocamento horizontal do gráfico da função para esquerda. No nosso caso, duas unidades para a esquerda, já que . Com isso, nossa função se tornará:
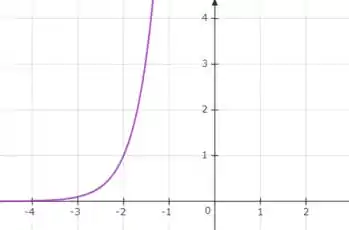
Repare que quando
Temos:
E prontinho, tempos nosso esboço do gráfico da função pedida.
Resposta
