Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 12
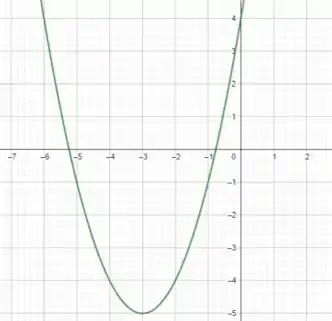
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na seção e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha??? Bom... a questão nos fala para fazer o gráfico da seguinte função:
Mas para isso, devemos utilizar as funções básicas dadas na seção .
Assim, vamos comparando com essas funções e assim vamos construindo o gráfico, certinho??
Vamos usar uma das funções da seção anterior como pede a questão, beleza?
Se ligue, man... uma das funções parecidas é:
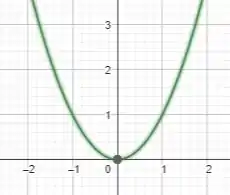
Então vamos analisar qual a diferença entre as duas funções para poder definir como será o gráfico, beleza?
Então bora lá!! 😉
Passo 2
Antes de tudo, a gente pode mudar um pouco a cara da nossa função de modo que a gente enxergue o que acontece nela.
Vamos primeiro somar com zero.. que também pode ser representado como :
Esse termo entre parênteses é um produto notável que pode ser reescrito assim:
Agora sim podemos comparar com .
Passo 3
Vamos primeiro analisar a função com o termo .
Bom.. a única diferença é aquele ali, que significa um deslocamento da parábola em unidades para esquerda.
Assim, temos :
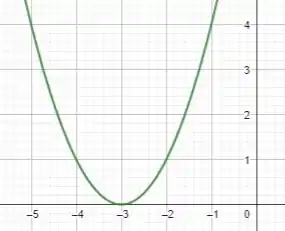
Passo 4
Por fim... sobrou aquele ali, que significa um deslocamento de unidades para o sentido negativo de .
Assim, temos a nossa função :
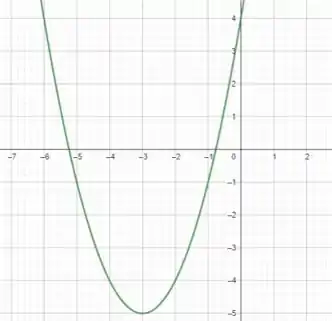
Entendeu direitinho?? Responde aee 😉
Resposta
