Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 18
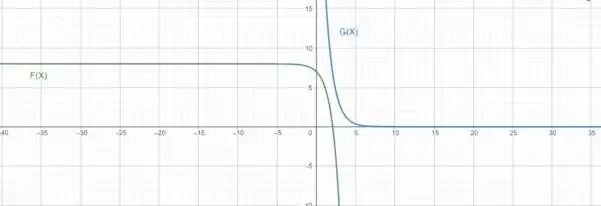
Começando com o gráfico de , encontre as equações dos gráficos que resultam ao
(a) refletir em torno da reta
(b) refletir em torno da reta .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
(a) Refletindo em torno da reta
Para refletir a função em torno da reta observe que a distância entre a função e a linha unidades.
Assim, para refletir a função em torno dessa linha, devemos mover cada ponto da função unidades na direção oposta à linha de reflexão.
Isso significa que devemos substituir por na função original, já que representa a distância entre a linha de reflexão e a função.
Portanto, a nova equação será:
Essa nova função representa a reflexão de em torno da linha
Nosso gráfico será representado da seguinte maneira (utilizado a ferramenta geogebra para plotar):
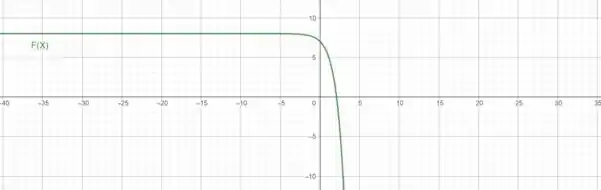
Passo 2
(b) Refletindo em torno da reta
Para refletir a função em torno da reta observe que a distância entre a função e a linha unidades.
Assim, para refletir a função em torno dessa linha, devemos mover cada ponto da função unidades na direção oposta à linha de reflexão.
Isso significa que devemos substituir por na função original, já que representa a distância entre a linha de reflexão e o eixo
Portanto, a nova equação será:
Essa nova função representa a reflexão de em torno da linha .
Nosso gráfico será representado da seguinte maneira (utilizado a ferramenta geogebra para plotar):
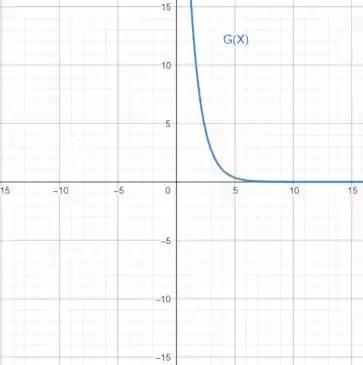
Prontinho! Conseguimos! 😉
Resposta
