Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.

Essa função tem a variável no denominador de fração. Isso nos lembra a função hiperbólica do tipo

A diferença é que temos no denominador. Isso que dizer que podemos usar essa função como nossa base.

No livro do Stewart, na Seção , temos o gráfico da função hiperbólica que é esse aqui:

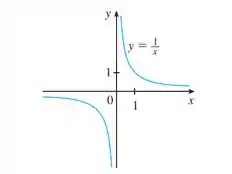
Repara que o gráfico se aproxima do eixo , mas nunca encosta nele. Quando isso acontece dizemos que a função possui uma assíntota vertical. Nesse caso, a nossa assíntota coincide com o eixo . Que é o mesmo que a reta .

Agora vamos entender o que devemos fazer para encontrar o gráfico da função .

Vamos fazer aqui uma pequena alteração, chamando .

Com isso a função que era:

Se torna

E esse gráfico a gente conhece do passo 2.

Agora vou te dar uma super dica. Sempre que isso puder ser feito, significa que está acontecendo um deslocamento horizontal da função.

Isso porque se

Teremos:

Ou seja, para conseguir o gráfico de , só precisamos deslocar a função hipérbole para a direita em unidades.

Uma soma o subtração junto ao sempre provoca um deslocamento na horizontal.

Assim, o gráfico resultante já vai ser a nossa resposta, dá só uma olhada:

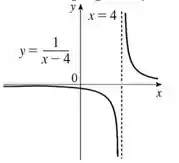
Dá para ver que a assíntota ficou deslocada né? Agora ela ta em , e isso acontece por causa do domínio da função: caso , teríamos que , o que ocasionaria em uma divisão por zero, algo proibido!. Logo, o valor não faz parte do domínio da função. Grava essas informações que lá nas próximas lições de cálculo é importante, fechou? ;)