Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.3 - Ex. 13

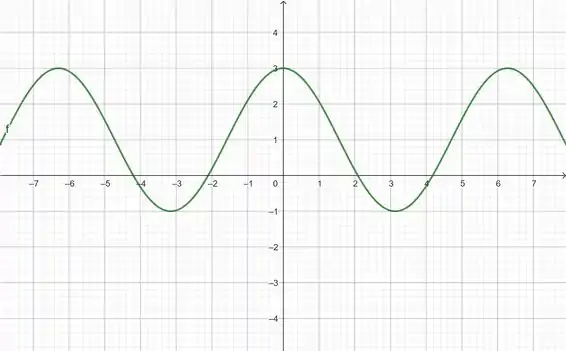
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.

Passo 1

Opa, bora resolver esse problema! Temos a seguinte função:

E precisamos construir um gráfico, mas não podemos ir fazendo isso ponto a ponto, iremos pegar um gráfico base, e iremos utilizar as propriedades de deslocamento de gráfico de uma função a partir de constantes e ai sim iremos encontrar o gráfico da função dada.

Para o nosso caso, temos duas propriedades:

Suponha que :

, desloca o gráfico de em unidades para cima;

Agora suponha que

, expanda o gráfico de verticalmente por um fator de ;

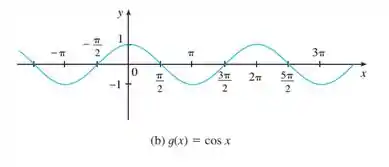
Na seção do Stewart nos é dado o gráfico da função cosseno, que é justamente com quem vamos trabalhar. Dá uma olhada:

Passo 2

Primeiro a gente tem que transformar esse gráfico no gráfico de

Para isso, só precisamos pegar e deformar ele na vertical, expandindo por um fator (isso é o que acontece quando multiplicamos toda a função por um número inteiro!).

Gráfico de

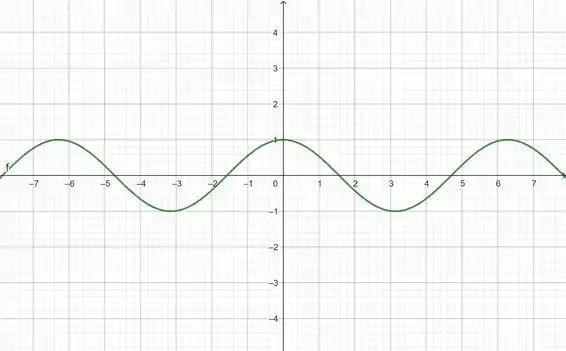
Vai ficar assim:

Gráfico de :

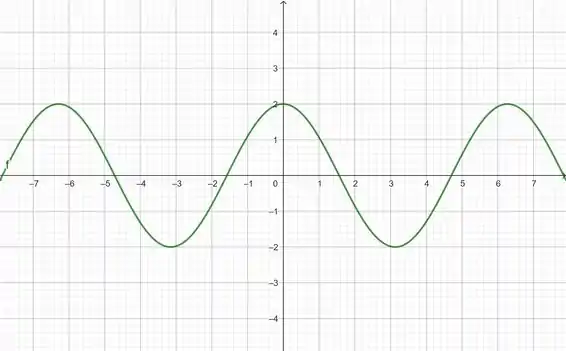
Passo 3

Agora, a gente vai pegar o gráfico de e deslocar ele para cima em uma unidade, que é o efeito produzido pela soma com o número (Toda vez que somamos um número com a nossa função, deslocamos ele para cima, fechou?).

Isso vai dar para a gente o gráfico de :

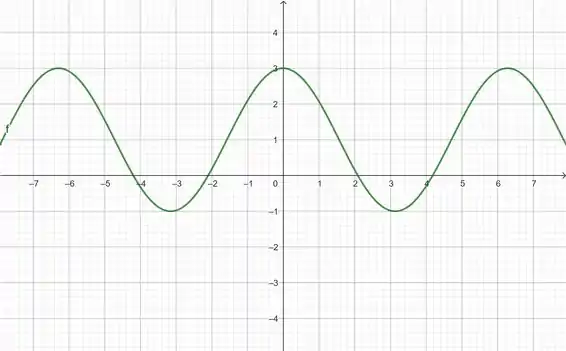
Pronto! Esse vai ser o gráfico de .

Uma última dica: Você pode fazer essas operações gráficas em qualquer ordem, belê? Se você deslocar ele primeiro e depois expandir, tem que dar a mesma coisa!