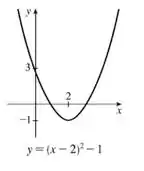
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
Eaee, belezinha?? Bom... queremos fazer o gráfico da seguinte função:
Para isso, o enunciado quer que utilizemos as funções básicas dadas na Seção para depois irmos aplicando as transformações até chegarmos na nossa função. Vamos então relembrar dessas funções da seção 1.2.
Tem funções polinomiais...

... funções raiz...
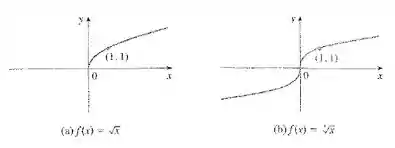
... funções algébricas de vários tipos...

... trigonom��tricas, exponenciais e logarítmicas...
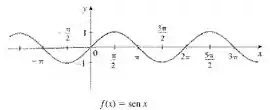
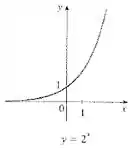
Mas no meio desse tanto de função, qual será a que a gente pode usar???
Bom, a nossa estratégia é comprar as funções. Qual é mais parecida? O que elas tem em comum e o que tem de diferente?
Bom, a nossa função é uma função polinomial de segundo grau. E qual é a função mais simples com essas características??
É dessa que vamos partir.
Passo 2
Pela Seção , temos o seguinte gráfico, que é o gráfico de uma função do segundo grau bem simples:
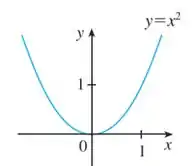
Vamos usar ela para encontrar o gráfico de mas, para isso, devemos dar uma arrumadinha na nossa função para escrevê-la de uma forma mais parecida com a nossa referência.
Vamos tentar fazer a aparecer um quadrado perfeito (assim como ). Então, a primeira coisa que iremos fazer é somar e subtrair do lado direito da equação:
Agora, iremos somar com :
Vamos olhar melhor para os três primeiros termos do lado direito:
Podemos escrever como sendo , que é o produto notável quadrado da diferença (não tira ele da cabeça que esse cara é importante que só em cálculo!).
Vim, achamos um quadrado perfeito!
Agora, substituímos na nossa equação:
As vezes dá um trabalhinho de olhar e perceber, mas relaxa que é só continuar estudando aqui pelo Responde Aí que fica tudo certo ;)
Passo 3
Agora que demos uma ajeitada na nossa função, ta mais fácil de saber como podemos alterar o gráfico de para virar o de .
Temos muitas formas de transformar as funções, podemos somar ou subtrair valores no , podemos multiplicar por constantes e etc... E cada operação vai dar um efeito no gráfico.
No geral, multiplicar por constantes dá efeitos de contração ou de esticar o gráfico em alguma direção. E somar a subtrações costumam gerar deslocamentos lineares.
Primeiro, iremos deslocar o gráfico para a direita em unidades pois temos uma subtração junto do , o que faz esse efeito, beleza? Saca só como vai ficar:
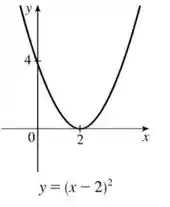
Passo 4
Agora temos e queremos transformar em . A diferença é que estamos subtraindo 1 de todos os valores.
Então nós temos que pegar o gráfico do passo anterior e deslocar ele para baixo em uma unidade.
Esse já vai ser o nosso gráfico final! Olha só no que vai resultar as nossas transformações:
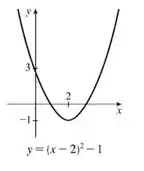
Resposta
O gráfico de vai ser: