Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 27

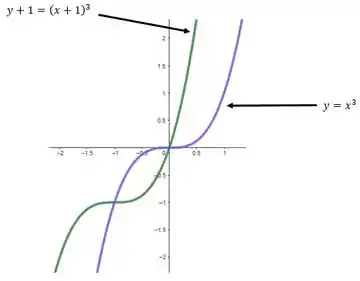
Dê uma equação para o gráfico transladado. Em seguida, faça um esboço dos gráficos originais e transladados juntos, identificando cada gráfico com sua equação

Esquerda 1, abaixo 1.

Passo 1

Vamos entender antes o que a questão nos pede. Primeiro, precisamos transladar a equação dada. Neste caso, ela deverá ser transladada para a esquerda em 1 unidade e para baixo em 1 unidade. É importante saber que a ordem das translações não afeta o resultado final. Sendo assim, será feito a translação horizontal inicialmente. Além disto, esses passos precisam ser realizados separadamente, e assim o faremos.

Em seguida, faremos um esboço do gráfico original e do resultado após ambas as translações.

Passo 2

Vamos começar a nossa solução realizando uma translação horizontal, que, neste caso, será em uma unidade para a esquerda. Dada uma função , para realizarmos uma translação horizontal, devemos substituir no lugar de , isto é, escrever:

Se for positivo, a translação será para a esquerda. Se for negativo, a translação será para a direita.

Sendo assim, como a questão nos pede para transladar a função em 1 unidade para esquerda, obtemos a seguinte função:

Passo 3

Para finalizarmos as operações da função, precisamos fazer uma translação vertical. Neste caso, a operação será feita com o . Semelhantemente do caso da translação horizontal, vamos substituir por . Isto é:

O que precisamos identificar agora é o sentido desta nossa translação e qual será o valor equivalente de . Valores positivos de indicam uma translação para baixo. Já valores negativos, indicam uma translação para cima.

Desta forma, para obtermos uma translação para baixo de 1 unidade, temos , e sendo assim, obtemos:

Passo 4

Agora, o que falta é realizar o esboço do gráfico. Este passo pode ser realizado através do uso de softwares, o qual ajuda na hora de realizar o seu plot, ou através da identificação da função e/ou utilizar o bom e velho método da tabela (valor de X versus valor de Y).

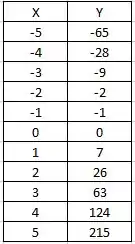
O esboço desta função é um pouco mais trabalhoso, visto que temos uma função polinomial. Sem o conhecimento de ferramentas mais avançadas de cálculo, devemos utilizar softwares e/ou o bom e velho método da tabela. Isto é, construímos uma tabela com os valores de X e os respectivos de Y e construímos o gráfico. Por exemplo, temos: