Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
No livro do Stewart, temos o seguinte gráfico:
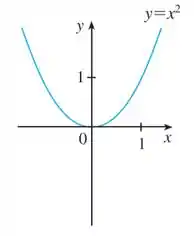
Esse é o gráfico de , o qual será a nossa base para as transformações.
E a partir dele, temos que chegar no gráfico de
Antes de dar uma mexida no gráfico, temos que mudar a nossa função para que ela se apareça apenas com a função .
Para isso, devemos fazer aparecer um quadrado perfeito na equação, aí a gente pode escrever ele na forma de um produto notável “quadrado da soma”.
Fazendo , temos:
Que é a função com o somado por “” unidades.
Passo 2
Ficou meio confuso? Dá uma olhada em como a gente faz, vou pegar e comparar com a fórmula desse produto notável:
Se compararmos a segunda expressão com a última, vemos que . Nosso produto notável vai ficar assim então:
Passo 3
Agora nós temos que reescrever a nossa função:
Temos que adicionar o junto com o para não aterarmos a equação (isso é o mesmo que somar com ). Olha o que podemos fazer agora:
Pronto! Usamos o que encontramos no passo anterior e escrevemos a nossa função de uma forma que podemos desenhar o gráfico muuuito mais facilmente!
Passo 4
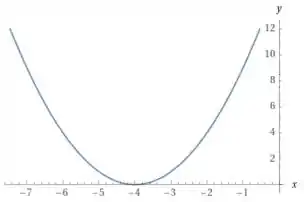
Primeiro, vamos pegar o gráfico e deslocar ele unidades para a esquerda.
Isso acontece por que somamos 4 unidades ao da função. Quando somamos ao andamos para a esquerda (e quando subtraímos ao andamos para a direita).
Assim, teremos o gráfico de :
Passo 5
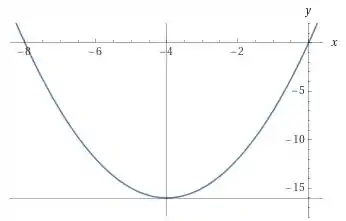
O próximo passo é deslocar o gráfico unidades para baixo.
Isso acontece pois estamos subtraindo 16 de toda a função. Daí, quando diminuímos toda a função por um valor, andamos com ela pra baixo. (e quando somamos toda a função por um valor, andamos com ela pra cima).
Assim a gente chega no gráfico de :
Passo 6
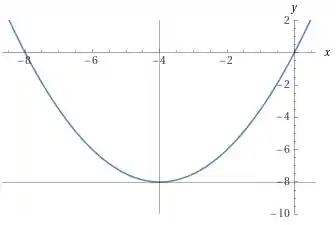
Ta acabando! Falta só o gráfico de .
Tudo o que precisamos fazer agora é pegar o gráfico anterior e comprimir ele na vertical por um fator . Compressão e expansão na vertical rola quando multiplicamos tooooda a expressão por um número.
O que vai rolar agora é que ao invés do vértice da parábola estar no , ele vai estar no .
Saca só:
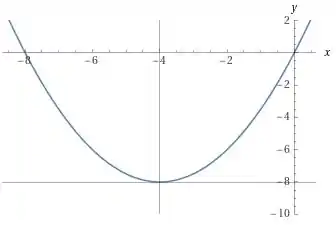
Uhul! Chegamos no noss resultado! Essa aqui já era ;)
Resposta
O gráfico de é o seguinte: