Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.3 - Ex. 10
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
E aí, preparado para mais essa questão?
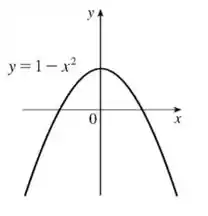
Nesse problema foi dada a função
E nosso objetivo é esboçar seu gráfico a partir dos gráficos dados na seção 1.2.
Parece complicado?
Basicamente, para resolver esse problema, vamos usar o gráfico de uma função cuja estrutura pareça com nossa função e aplicar algumas manipulações de translação e rotação do gráfico para esboçar o gráfico da nossa função.
Veja só!
Passo 2
Perceba que nossa função é uma parábola já que aparece apenas uma vez e elevado a ...
No livro do Stewart, podemos ver o gráfico de na seção :
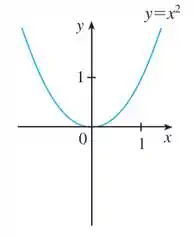
É uma parábola, referente a uma função do segundo grau, e a expressão que ta na Figura lembra um pouquinho a nossa né?
Primeiro, vamos transformar o gráfico de no gráfico de .
Para isso, a gente tem que refletir o gráfico de com relação ao eixo . Dá uma olhada em como vai ficar:
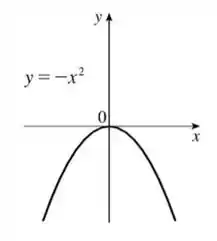
Tranquilo até aqui?
Passo 3
O próximo passo é obter a partir e .
Tudo o que precisamos fazer é deslocar o gráfico de uma unidade para cima, fechou? Saca só:
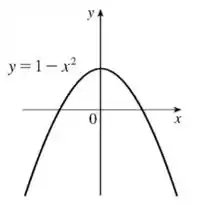
Pronto! Esse aí vai ser o nosso gráfico final ;)
O que achou? Responde Aí!
Resposta
O gráfico de vai ser:
