Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 32
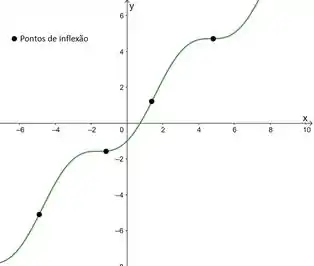
Faça um gráfico completo de indique os limites quando e localize todos os extremos relativos, os pontos de inflexão e as assíntotas (quando apropriado).
Passo 1
Vamos começar calculando os limites:
Podemos usar o teorema do confronto. Sabemos que:
Fazendo o mesmo para o outro limite:
Com isso a gente vê também que não há assíntotas horizontais.
Passo 2
Para localizar os extremos relativos, precisamos calcular os valores de quando
Vamos fazer o teste da derivada segunda para classificar esses pontos:
Ih deu . Vamos olhar o sinal da derivada antes e depois do ponto:
Como a derivada é positiva antes e depois do ponto, esse não é um ponto de máximo nem de mínimo.
Logo, não temos extremos relativos.
Passo 3
Os pontos de inflexão ficam onde . Vamos achar todos eles:
Assim:
Esses vão ser nossos ponto de inflexão.
Passo 4
Vamos verificar os pontos de descontinuidade de para descobrir se existem assíntotas verticais. Só repara uma coisa:
Nossa função é uma subtração entre duas funções contínuas. Pelas propriedades de continuidade, ela também será uma função contínua.
Por isso, não há assíntotas verticais.
Passo 5
Agora é fazer o gráfico com tudo isso que a gente achou:
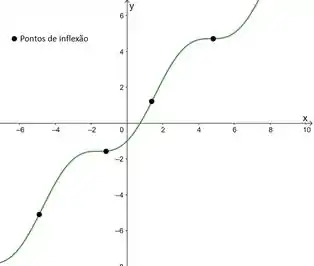
Resposta
Não há extremos relativos
Pontos de inflexão quando
Não há assíntotas
