Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.2 - Ex. 70
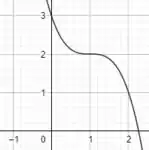
Faça o gráfico da função:
Comece pelo gráfico de uma das funções padrão apresentadas nas figuras 1.14-1.17 e aplique a mudança adequada.
Passo 1
Galera, dentre as funções apresentadas na seção 1.1 do George, a função que mais se aproxima da que temos é a seguinte:
Cujo gráfico é:
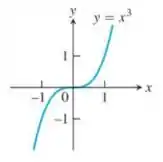
No entanto, a função original tem um sinal negativo, não é? Quando aparece esse sinal significa que o gráfico dessa função vai ser refletido em torno do eixo . Dessa forma, a função que mais se assemelha à que temos é , que apresenta o seguinte gráfico:
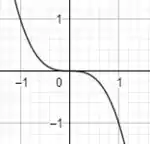
Passo 2
Agora que encontramos uma função semelhante à original, basta irmos inserindo as informações da nossa função original na função que estamos usando como referência, tudo bem? Fica tranquilo, faremos as inserções aos poucos!
Primeiramente devemos somar 1 unidade diretamente na nossa variável . Quando nossa variável é negativa (como é o nosso caso), ao somarmos um valor diretamente na variável isso faz com que o gráfico da função seja deslocado para a direita. Como há uma soma de 1 unidade, então isso implica que o gráfico vai ser deslocado de 1 unidade para a direita. Logo, a função teria o seguinte gráfico:
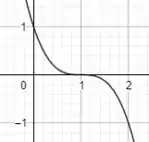
Passo 3
Agora só falta um passinho para finalizarmos o gráfico! A última coisa que falta é somarmos 2 unidades na função. Quando há uma soma na função, isso implica que o gráfico vai ser deslocado para cima, beleza? Dessa forma, a nossa função final teria um gráfico assim:
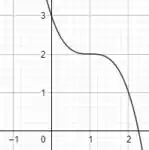
Resposta
O gráfico de é:
