Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 6
a) Faça o gráfico da função
b) Estime a área sob o gráfico de usando quatro retângulos aproximantes e tomando como pontos amostrais as extremidades direitas e os pontos médios. Então, aperfeiçoe sua estimativa utilizando seis retângulos aproximantes. Esboce a curva e os retângulos aproximantes.
c) Aperfeiçoe suas estimativas da parte usando oito retângulos.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente fazer o gráfico da função , no intervalo , e depois estimar a área sob o gráfico usando retângulos aproximantes e tomando como pontos amostrais as extremidades direitas e os pontos médios. Em seguida, vamos aperfeiçoar nossa estimativa utilizando e depois retângulos aproximantes.
Pra isso, precisamos lembrar que a área sob a curva pode ser aproximada pelo somatório:
Onde , sendo o número de retângulos aproximantes e nosso intervalo. Então, vamos lá!
Passo 2
Vamos começar esboçando o gráfico da função :
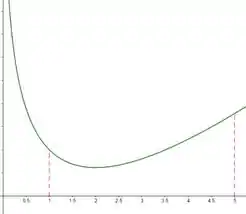
Observe que as linhas tracejadas estão delimitando nosso intervalo . Agora vamos usar o gráfico para estimar a nossa área, certo?
Passo 3
Precisamos estimar a área usando quatro retângulos, ou seja, . Perceba que da nossa fórmula e . Dessa forma, temos:
Vamos então considerar os intervalos:
Tranquilo até aqui?
Passo 4
Vamos resolver o item i) da letra b). Isto é usar como pontos amostrais as extremidades direitas.
Da definição, nós temos que esses pontos são dados por:
Dessa forma, para , vamos ter e . Então, substituindo na fórmula, ficamos com:
Olhando no gráfico, vamos extrair os em cada ponto:
Que corresponde à área referente aos retângulos abaixo:
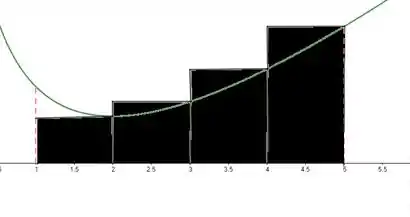
Show?
Passo 5
Agora, vamos usar os pontos médios dos intervalos . Ou seja:
Desenhando os retângulos, temos:
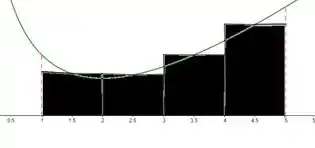
Substituindo na e na fórmula, temos:
Olhando no gráfico, temos os correspondentes de cada :
Está acompanhando?
Passo 6
Agora vamos usar 8 retângulos. Então, nosso vai mudar porque teremos :
Agora vamos definir nossos intervalos:
Beleza, vamos usar como pontos amostrais as extremidades direitas. Então, nossos pontos, dados por , serão:
.
Daí, substituindo na fórmula, temos:
Olhando no gráfico, obtemos:
Fazendo a soma:
Essa é a área correspondente aos retângulos abaixo:
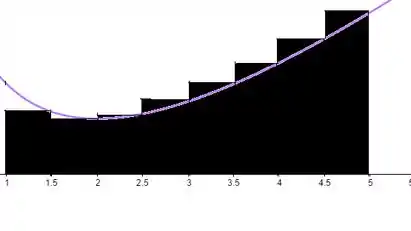
Estamos quase no fim!
Passo 7
Agora vamos usar os pontos médios dos intervalos, ou seja, .
Substituindo isso na fórmula do somatório:
Olhando no gráfico, temos:
Que corresponde a área dos retângulos:
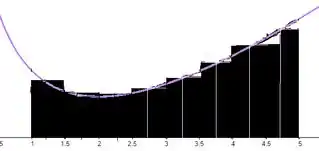
É isso! O que achou? Responde Aí!