Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 5c
É dado o gráfico de uma função .Estime usando cinco subintervalos com
- Pontos médios
Passo 1
Eaeee, belezinha??? Bom... queremos estimar a integral
Usando subintervalos (utilizando os pontos médios) da seguinte função:
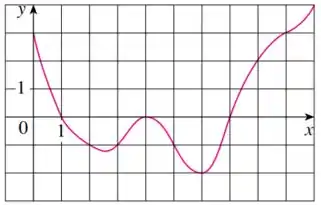
Para isso, devemos utilizar a soma de Riemann.
Tá.... mas o que é essa soma??
Bom... a soma de Riemann para uma função em um intervalo fechado com subintervalos é expressa como:
Onde:
- é um ponto amostral no -ésimo subintervalo;
- é a largura do -ésimo subintervalo .
Agora vamos aplicar!! 😉
Passo 2
Bom... selecionando os pontos médios em subintervalos, temos:
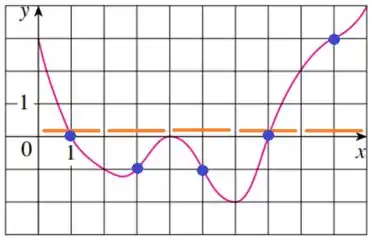
Pelos pontos marcados podemos concluir que:
Agora vamos aplicar a soma de Riemann!!
Passo 3
Daí, temos que:
Logo,
Ou seja
Entendeu direitinho?? Responde aee 😉
Resposta
Exercícios de Livros Relacionados
O gráfico da velocidade de um carro freando é mostrado. Use-o para estimar a distância percorrida pelo carro enquanto os freios estão sendo aplicados.
Quando estimamos as distâncias a partir dos dados das velocidades, algumas vezes é necessário usar tempos t 0 ,t 1 ,t 2 ,t 3 , ... que não estão igualmente espaçados. Podemos ainda estimar as distânci
A leitura do odômetro de uma motocicleta em intervalos de 12 segundos é mostrada na tabela a seguir.Estime a distância percorrida pela motocicleta durante esse período, usando a velocidade no começo d
Alguns sistemas algébricos computacionais têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, no mínimo se x i * é um extremo esquerdo ou direito.Se f x = x , 1 ≤ x ≤ 4
Se f x = sen sen x ,0 ≤ x ≤ π / 2 , use os comandos discutidos no Exercicio 9 para encontrar as somas esquerda e direita para n = 10 , 30 e 50 .Ilustre fazendo o gráfico dos retângulos da parte (a