Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 107
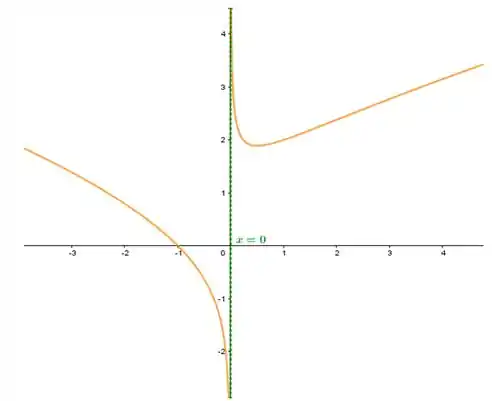
Faça o gráfico da função
Explique a relação entre a fórmula e o que você observa.
Passo 1
O primeiro passo é considerar e observar o que essa função tem a nos “dizer”.
Para isso precisamos reescrever . E isso pode ser feito calculando o MMC , ou seja,
Utilizando a regra de multiplicação de potências, teremos que,
Utilizando o famoso “quem tá no sol vai para sombra e quem está sombra vai para o sol” temos que , então
Sendo assim,
Passo 2
O segundo passo é perceber que ao olharmos , veremos que estamos com uma divisão de funções, que tem um “probleminha” quando , ou seja, quando substituirmos esse número na função o denominador zera.
Passo 3
O terceiro passo é notar que quando isso acontece significa que possui uma assíntota vertical. Porém, é necessário verificar se isso é verdade, ou seja, precisamos ver se, .
O que é simples de verificar pois só precisaremos substituir em cada um dos limites laterais e ver o que acontece,
E,
Isso acontece pois quando estamos lidando com números negativos, que a depender da proximidade do zero serão menores que 1 ocasionando assim, que o numerador seja positivo. Como a raiz cúbica de um número negativo é sempre negativa, teremos pela regra sinal que o resultado final desse limite será negativo.
Com isso, possui uma assíntota vertical em .
Resposta
possui uma assíntota vertical em
