Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 99
Faça o gráfico da função e inclua o gráfico e a equação das assíntotas
Passo 1
O primeiro passo é relembrar que para encontrar assíntotas oblíquas primeiro precisamos olhar para o numerador e caso ele tenha 1 grau a mais que o grau do denominador então a possuirá uma assíntota obliqua.
Considerando e observando a função,
Vemos que o polinômio de cima tem grau 2, e o grau do polinômio de baixo é 1, ou seja, o de cima tem um grau a mais que o de baixo, então possui assíntota oblíqua.
Passo 2
O segundo passo é dividir o polinômio de cima pelo polinômio de baixo e podemos fazer armando uma conta de dividir como aprendemos quando éramos criança
Para isso precisamos lembrar que em uma divisão de polinômios é um pouco diferente da normal, o termo que fica no quociente multiplica todos o termo do dividendo e o resultado
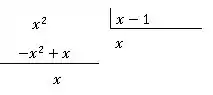dessa multiplicação inverte de sinal ,
Queremos cancelar o , colocamos no quociente, pois quando multiplicássemos ele por o resultado pois inverte o sinal, e assim cancelaria o sobrando apenas o Continuando a conta com a mesma regra,
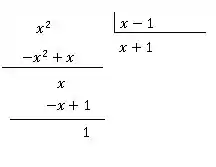
Passo 3
O segundo passo é reescrever de acordo com o que obtemos na divisão do item 1, ou seja,
Onde é linear e é o resto
Estamos interessados em saber se quando o limite de o (resto) vai para zero, quando isso acontece significa que a distância entre e é quase zero. Então vamos verificar.
Conseguiremos fazer isso dividindo pela maior potência de ,
utilizando a regra do quociente (o limite da divisão é a divisão dos limites) e a regra da subtração (limite da subtração é a subtração dos limites),
Como o limite deu zero, então é uma assíntota oblíqua para . E podemos reescrever como a soma da , ou seja,
Passo 4
Perceba que o denominador da função se anula para . Então temos um assíntota vertical.
Vejamos que acontece com a função à direita e à esquerda desse ponto. Ou seja, vamos calcular e .
Bora lá,
utilizando a regra do quociente (o limite da divisão é a divisão dos limites) e a regra da subtração (limite da subtração é a subtração dos limites),
Vamos analisar se esse limite vai para ou . Beleza?
Como estamos nos aproximando de 1 pela direita, ou seja, valores maiores que um, o denominador fica positivo. E assim, teríamos,
Passo 5
Por outro lado, usando as mesmas regras,
utilizando a regra do quociente (o limite da divisão é a divisão dos limites) e a regra da subtração (limite da subtração é a subtração dos limites),
Vamos analisar se esse limite vai para ou . Beleza?
Como estamos nos aproximando de 1 pela esquerda, ou seja, valores menores que um, o denominador fica negativo. E assim, teríamos,
Resposta
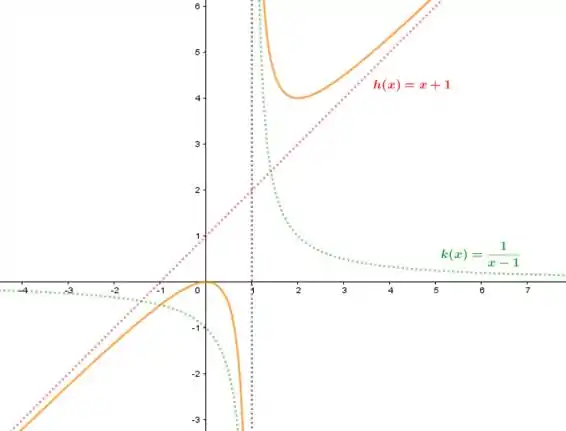
E é uma assíntota para E x=1
E