Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 26
Neste exercício, consideramos a família de funções , onde é um inteiro positivo.
a) Faça o gráfico das funções e , na mesma tela usando a janela retangular por .
b) Faça o gráfico das funções e na mesma tela usando a janela retangular dada na parte (a).
c) Faça o gráfico de todas as funções das partes (a) e (b) na mesma tela, usando a janela retangular por .
d) Que conclusões você pode tirar desses gráficos?
Passo 1
Fala pessoal, tudo bem? O problema nos deu essa função genérica aqui
Que é da família das hipérboles. No primeiro item precisamos fazer o gráfico de duas hipérboles com potência ímpar, e no segundo item duas hipérboles com expoentes pares. A ideia é verificar onde elas estão localizadas e a diferença entre as paridades das potências nos gráficos.
No fim, precisamos fazer os gráficos juntos das hipérboles, para verificar se a janela proposta é adequada para ver todo o comportamento e quais semelhanças e diferenças entre os gráficos. Mas relaxa, vou fazer com você!
Passo 2
No item (a) devemos esboçar o gráfico das funções e na janela por :
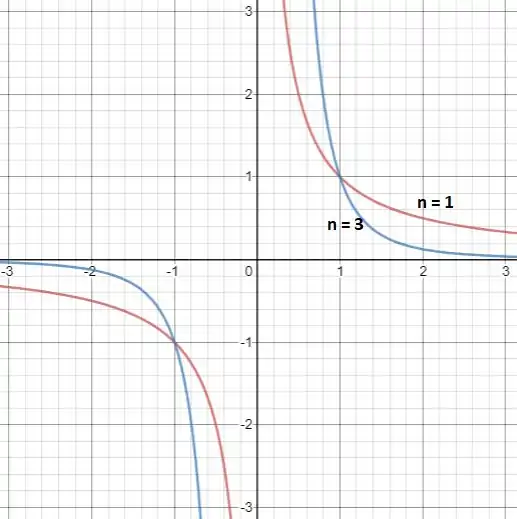
Vemos que a janela é adequada e os gráficos tem comportamentos parecidos, estando ambos nos quadrantesímpares! Beleza?
Passo 3
No item (b), devemos plotar as funções com e na mesma janela do item (a):
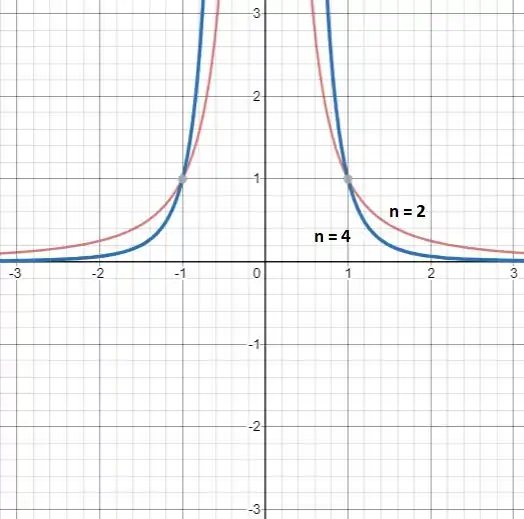
Vemos que a janela também é adequada para ver os comportamentos. Ambos os gráficos ocupam os quadrantes em que , pois as potências de são pares, e qualquer valor negativo de retorna um valor positivo de imagem
Passo 4
Por fim, no item (c), temos que plotar todas as funções na janela por :
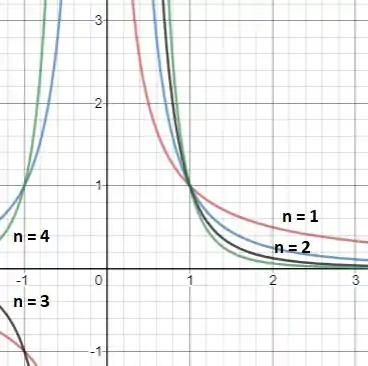
Para par, a função é par, enquanto para ímpar, ela é ímpar. Além disso, vemos que a janela reduzida do item (c) não cobre bem os gráficos em toda sua extensão!
Resposta
Esboço de gráfico. Além disso, vemos que a janela reduzida do item (c) não cobre bem os gráficos em toda sua extensão.