Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 36
O primeiro gráfico da figura a seguir é aquele que uma calculadora gráfica TI-83 exibe como função . Ele está incorreto e, portanto, para ajudar a explicar sua aparência, redesenhamos a curva em questão no modo pontual da calculadora, obtendo o segundo gráfico.
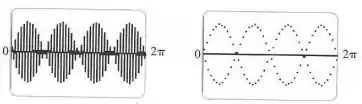
Que duas curvas senoidais a calculadora parece estar desenhando? Mostre que cada ponto do gráfico de que a TI-83 escolhe para desenhar, de fato, em uma dessas curvas.
Passo 1
Oie, vou te ajudar a resolver essa atividade.
Ela é um confusa, mas vamos tentar dar uma esclarecida.
Esse problema aqui é mais técnico e envolve o funcionamento de calculadoras gráficas.
Nos é dito que a calculadora esta plotando os pontos errados do gráfico de:
Precisamos então entender, a partir da janela de visualização da calculadora, qual era sua intenção ao plotar o gráfico. Precisaremos analisar o comportamento da quantidade de pixels que ela
No caso, a janela da calculadora TI-83 é de pixels de largura. Como queremos plotar o gráficos no intervalo considerando o primento ponto marcado como e o último como , existirão intervalos entre pontos marcados pela calculadora.
O tamanho desses intervalos será
Assim, os valores plotados pela calculadora serão nos pontos
Passo 2
Quando plotamos , os pontos plotados são:
Mas note que,
Assim, como :
Logo,
Portanto, os pontos marcados para a curva são os mesmos que os marcados para as curvas: