Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 28
Fazer um esboço do gráfico de , determinando:
. Os extremos relativos de ;
. Os pontos de inflexão do gráfico de ;
. Os intervalos onde é crescente e aqueles nos quais é decrescente;
. Onde o gráfico é côncavo para cima e onde é côncavo para baixo;
Da função
Passo 1
Legal gente, sem pânico! Temos milhões de coisas pra calcularmos, então vamos ser organizados e dividir tudo em pequenos passos de cada vez. A primeira coisa que a questão nos pede, é que determinemos os extremos relativos de f. Para isso, temos que:
- Fazer a primeira derivada e igualar a 0 para achar um c
- Fazer a segunda derivada e realizar um teste para determinamos se é um extremo ou mínimo relativo.
Então, nossa função é dada por:
Derivando e igualando a 0, temos que:
Resolvendo essa equação, temos que a raíz é:
Então temos 1 C. Vamo aos testes! A segunda derivada da função é igual a:
Aplicando as raízes, temos que:
-p/ :
Indeterminação, logo, não existe máximo ou mínimos relativos.
Passo 2
Ufa, primeira parte já foi! Para a segunda parte, precisamos definir o nosso ponto de inflexão. Resumindo, vamos derivar 3 vezes e achar esses pontos? PREPARADOS? SIMBORA!
Neste ponto, igualamos a 0 e temos nossos primeiros candidatos a pontos de inflexão.
Não existem raízes! Logo, não existem pontos de inflexão!
Passo 3
E vamos seguindo o rumo galera! Para determinamos a região aonde a nossa curva cresce e decresce, é bem simples. Derivamos uma vez, achamos os 0 e comparamos os intervalos dos 0. Como assim? Vamos lá.
Para a nossa função, temos que a primeira derivada é igual a
A raiz dessa equação é “-2”
Então, vamos analisar essa função em 2 momentos distintos:
Para
Para esse caso, nossa função fica negativa, indicando então DECRESCIMENTO
Para
Para esse caso, nossa função fica positiva, indicando então CRESCIMENTO
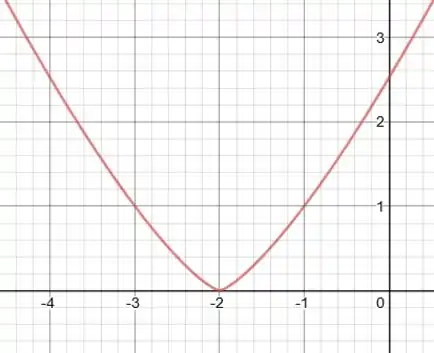
Passo 4
Como não temos pontos de inflexão, não temos concavidades.
Resposta
Sem pontos de inflexão
Para
Para esse caso, nossa função fica negativa, indicando então DECRESCIMENTO
Para
Para esse caso, nossa função fica positiva, indicando então CRESCIMENTO