A figura mostra um arco de círculo com comprimento s e uma corda com comprimento d, ambos subentendidos por um ângulo central u. Encontre
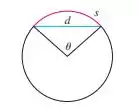
Passo 1
Fala aeee, tranquilo??
Bom, se temos que calcular:
Primeiro, vamos encontrar quem é e quem é , certo?
Passo 2
Bom, é o comprimento do arco e temos o ângulo central . Então, por definição:
Essa é uma fórmulinha muito boa de se trazer consigo.
Passo 3
Para , vamos pegar o triângulo retângulo:
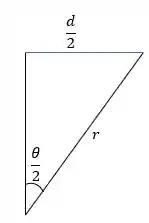
Dele, podemos tirar a relação:
Passo 4
Substituindo e no limite:
Opa, podemos arrumar isso:
Isso te lembra algum limite?? Bom, me lembra ao fundamental:
E não é à toa: esses limites são recíprocos. Pelo fato de que , podemos dizer que:
E é só isso. Acabamos hehe.