Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 2
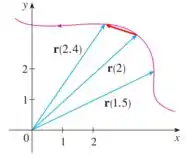
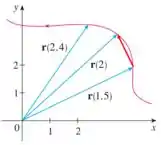
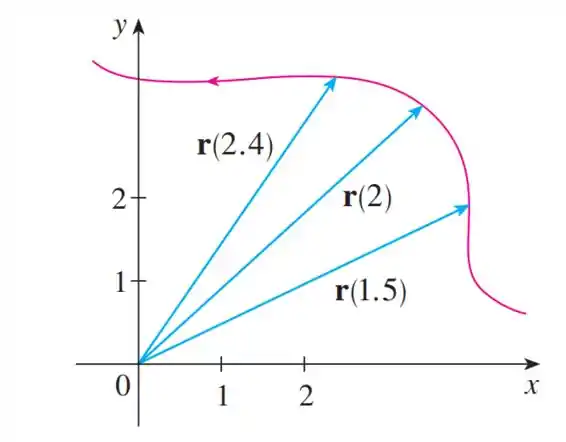
A figura mostra a trajetória de uma partícula que se move com vetor posição no instante .
- Desenhe um vetor que represente a velocidade média da partícula no intervalo de tempo .
- Desenhe um vetor que represente a velocidade média da partícula no intervalo de tempo .
- Escreva uma expressão para o vetor velocidade .
- Desenhe uma aproximação do vetor e estime a velocidade escalar da partícula em .
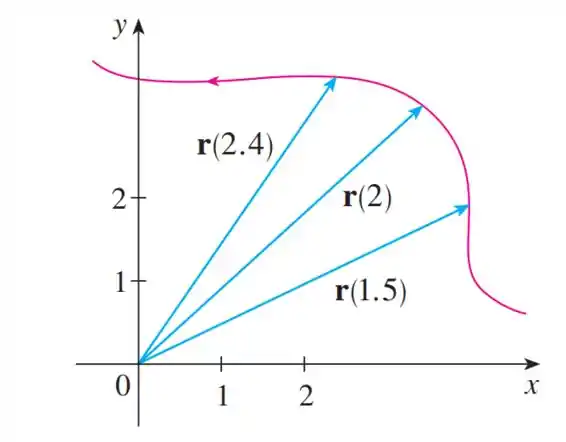
Passo 1
Olá, tudo bem? Vou te ajudar a resolver essa atividade. Fica tranquilo que vai da tudo certo.
O vetor velocidade vai ser dado por:
Isso é, precisaremos ligar o ponto:
Ao ponto de:
Então para os casos em que temos:
A gente liga então o vetor velocidade de ao vetor velocidade de .
A velocidade média no ponto, é dada pelo limite da equação do espaço naquele ponto, então iremos utilizar esse conceito para encontrarmos uma equação para .
Passo 2
-
No intervalo temos:
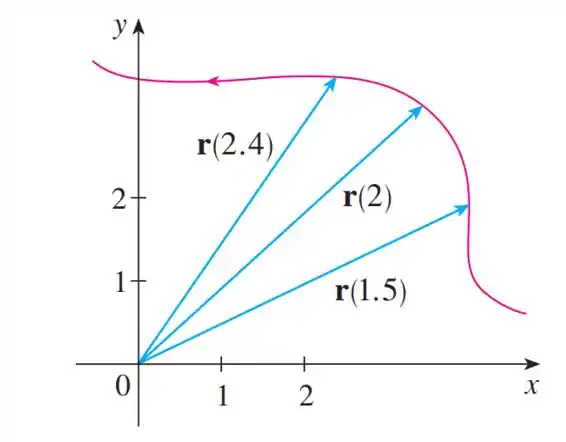
Passo 3
-
No intervalo temos:
Passo 4
-
A velocidade média pode ser determinada através do limite:
Mas esse limite também pode ser representado por:
Isso é, a derivada da equação do espa��o no ponto .
Passo 5
Uma representação gráfica seria um vetor indo de até :
é tangente à curva em , pois esse é o significado da derivada em um ponto, e aponta na direção do aumento de . Seu comprimento é a velocidade da partícula em.
Podemos estimar a velocidade ao fazer a média dos comprimentos dos vetores encontrados nas partes (a) e (b), que representam a velocidade média sobre e respectivamente.
Usando a escala dos eixos como guia, estimamos que os vetores tenham comprimentos de e . Assim, estimamos a velocidade em :
