Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 1

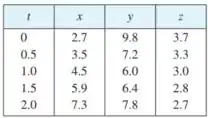
A tabela fornece coordenadas de uma partícula movendo-se no espaço ao longo de uma curva lisa.

  1. Determine a velocidade média nos intervalos de tempo 0 ; 1 ,   0,5 ; 1 , 1 ; 2   e   1 ; 1,5 .
  2. Estime a velocidade escalar da partícula no instante t = 1 .

Passo 1

Fala aí pessoal. Trânquilo?

O objetivo desta questão é determinar a velocidade média de uma partícula que se move no espaço ao longo de uma curva lisa em diferentes intervalos de tempo e estimar a velocidade escalar da partícula em um instante específico.

Na letra A, temos que lembrar que a velocidade média da partícula em um intervalo de tempo [ t 1 , t 2 ] é definida como a distância percorrida dividida pelo tempo total do intervalo. Considerando que a partícula tem coordenadas ( x ( t ) , y ( t ) , z ( t ) ) em função do tempo t , a fórmula para a velocidade média v m é d i a ​ em um intervalo de tempo [ t 1 , t 2 ] é:

v m é d i a = x t 1 - x t 2 + y t 1 - y t 2 + z t 1 - z t 2 t 2 - t 1

E na letra B, temos que obter a velocidade escalar, e para isso precisamos calcular o módulo da velocidade média nos pontos pedidos

Para encontrar a velocidade média

v → t = 1 = v m é d i a 0.5,1 + v m é d i a 1,1.5 2

E calcular seu módulo

v = x 2 + y 2 + z 2

Agora é só resolver!

Passo 2

Olá, tudo bem? Você lembra que a velocidade média é dada por:

v → = Δ r → Δ t

v m é d i a = x t 1 - x t 2 + y t 1 - y t 2 + z t 1 - z t 2 t 2 - t 1

Substituindo os intervalos

  • No intervalo de [ 0 ; 1 ] temos:

    • v → = 4,5 - 2,7 ; 6 - 9,8 ; 3 - 3,7 1 - 0

    v → = 1,8 ; - 3,8 ; - 0,7

    Temos então

    v → = 1,8 i → - 3,8 j → - 0,7 k →

  • No intervalo de [ 0,5 ; 1 ] temos:

    • v → = 4,5 - 3,5 ; 6 - 7,2 ; 3 - 3,3 1 - 0,5

    v → = 1 ; - 1,2 ; - 0,3 0,5

    v → = 2 ; - 2,4 ; - 0,6

    Temos então

    v → = 2 i → - 2,4 j → - 0,6 k →

  • No intervalo de [ 1 ; 2 ] temos:

    • v → = 7,3 - 4,5 ; 7,8 - 6 ; 2,7 - 3 2 - 1

    v → = 2,8 ; 1,8 ; 0,3 1

    v → = 2,8 ; 1,8 ; 0,3

    Temos então

    v → = 2,8 i → + 1,84 j → + 0,3 k →

  • No intervalo de [ 1 ; 1,5 ] temos:

v → = 5,9 - 4,5 ; 6,4 - 6 ; 2,8 - 3 1,5 - 1

v → = 1,4 ; 0,4 ; - 0,2 0,5

v → = 2,8 ; 0,8 ; - 0,4

Temos então

v → = 2,8 i → + 0,8 j → - 0,4 k →

Passo 3

A velocidade média pode ser determinada através da média aritmética das velocidades nos intervalos 0,5   ; 1 e   [ 1 ; 1,5 ] .

v → m e d = 2 ; - 2,4 ; - 0,6 + 2,8 ; 0,8 ; - 0,4 2

v → m e d = 4,8 ; - 1,6 ; - 1 2

v → m e d = 2,4 ; - 0,8 ;   - 0,5

E a velocidade escalar vai ser o módulo desse vetor:

v = 2,4 2 + - 0,8 2 + - 0,5 2

v = 2,58

Resposta

a v → = 1,8 ; - 3,8 ; - 0,7

v → = 2 ; - 2,4 ; - 0,6

v → = 2,8 ; 1,8 ; 0,3

v → = 2,8 ; 0,8 ; - 0,4  

b v m e d = 2,58

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule os limites. lim t → 0⁡ e - 3 ti + t 2 s e n 2 tj + cos ⁡ 2 t k
Determine o domínio das funções vetoriais. r t = t - 2 t + 2i + s e ntj + ln ⁡ ( 9 - t 2 )k
Suponha que u e v sejam funções vetoriais que possuem limites quando t → a e seja c uma constante. Demonstre as seguintes propriedades de limites.(a) lim t → a ⁡ u t + v t = lim t → a ⁡ u t + lim t →
Determine as componentes tangencial e normal do vetor aceleração. r t = cos ⁡ t i + sen ⁡ t j + t k
Determine as componentes tangencial e normal do vetor aceleração. r ( t ) = 1 + t i + t 2 - 2 t j