Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 54

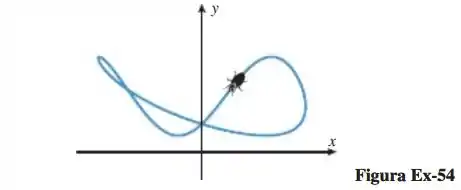
A figura a seguir mostra a trajetória de uma mosca cujas equações do movimento são

x = cos ⁡ t 2 + s e n t ,           y = 3 + s e n 2 t - 2 s e n 2 t ,           0 ≤ t ≤ 2 π

a Quais são os pontos mais alto e mais baixo do voo?

b A que distância à esquerda e à direita da srcem ela voa?

Passo 1

Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?

Bom, para esse exercício em específico, precisamos usar as definições e usos das derivadas. Nesse caso em questão, temos que verificar o comportamento da função e ver os pontos de máximo e mínimo valor em cada eixo.

Usando a derivada, podemos verificar se a função é crescente ou decrescente em um dado intervalo. Ainda, igualando a zero, conseguimos verificar os pontos críticos em que a função tem valor mínimo ou máximo.

Passo 2

Então, para encontrar os pontos mais alto e mais baixo do voo, ou seja, os pontos máximo e mínimo do eixo y , iremos aplicar a definição de derivada para a equação desse eixo para encontrar esses pontos. Logo, teremos:

y = 3 + s e n 2 t - 2 s e n 2 t

Tal que:

y ' = 2 cos ⁡ 2 t - 4 cos ⁡ t s e n t

Ou ainda:

y ' = 2 cos ⁡ 2 t - 2 s e n 2 t

y ' = 2 cos ⁡ 2 t - s e n 2 t

Passo 3

Dessa forma, igualando esse resultado a zero:

y ' = 2 cos ⁡ 2 t - s e n 2 t = 0

Isso pode ser reescrito dividindo ambos os lados por 2 :

cos ⁡ 2 t - s e n 2 t = 0

Isso mostra que:

cos ⁡ 2 t = s e n 2 t

Temos os pontos críticos em:

t = π 8 , t = 9 π 8 , t = 5 π 8 , t = 13 π 8

Então, pegando estes ponto críticos e verificando o valor da função em cada um, iremos ter os seguintes valores:

y π 8 = y 9 π 8 = 3,4142

E:

y 5 π 8 = y 13 π 8 = 0,5858

Portanto, o maior resultado é o ponto máximo (mais alto do voo) e o menor resultado é o ponto mínimo (mais baixo do voo).

Passo 4

Da mesma forma, iremos aplicar o mesmo método para encontrar os valores à esquerda e à direita do eixo, ou seja, os pontos máximo e mínimo do eixo x .

Dessa forma, derivando a equação de x :

x = cos ⁡ t 2 + s e n t → x ' = 2 + sent - sent - cos 2 ⁡ t 2 + s e n t 2

Ou seja:

x ' = - 2 s e n t - s e n 2 t - cos 2 ⁡ t 2 + s e n t 2

Lembrando da identidade trigonométrica:

s e n 2 x + c o s 2 x = 1

Podemos substituir na primeira derivada, tal que:

x ' = - 2 s e n t - s e n 2 t + cos 2 ⁡ t 2 + s e n t 2 = - 2 s e n t - 1 2 + s e n t 2

Os seus pontos críticos serão dados por:

x ' = - 2 s e n t - 1 2 + s e n t 2 = 0

E isso mostra que:

s e n t = - 1 2

Logo:

t = 7 π 6 ,   t = 11 π 6

E os valores de x nesses pontos são dados por:

x 7 π 6 = - 0,5774

E

x 11 π 6 = 0,5774

Analogamente, o maior resultado é o ponto mais à direita e o menor resultado é o ponto mais à esquerda.

Resposta

a Ponto mais alto: y = 3,4142

Ponto mais baixo: y = 0,5858

b À esquerda: x = - 0,5774

À direita: x = 0,5774

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar os máximos e mínimos das seguintes funções, nos intervalos indicados.k) f x = s e n 3 x - 1 ,0 , π 2
Determinar os máximos e mínimos das seguintes funções, nos intervalos indicados.e) f x = x 1 + x 2 ,- 2 ,2
Encontrar os intervalos de crescimento, decrescimento, os máximos e os mínimos relativos das seguintes funções:d) h x = 1 3 x 3 + 1 2 x 2 - 6 x + 5
Encontrar os intervalos de crescimento, decrescimento, os máximos e os mínimos relativos das seguintes funções:b) f x = 3 x 2 + 6 x + 1
Determinar os máximos e mínimos das seguintes funções, nos intervalos indicados.a) f x = 1 - 3 x ,- 2 ,2