Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 52
A concentração de uma droga na corrente sanguínea horas após ter sido injetada é usualmente modelada por uma equação da forma
onde e .
- Em que momento ocorre a concentração máxima?
- Para simplificar, tome ; use um recurso gráfico computacional para verificar seu resultado da parte (a) fazendo o gráfico de para vários valores de e .
Passo 1
- Vamos lá, encontramos a concentração máxima derivando a função e igualando a zero, vamos fazer isso:
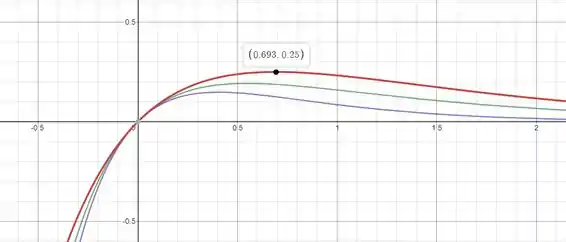
- Vamos plotar o gráfico usando , e , depois , e e , e temos:
Igualando a zero:
Vamos aplicar o logaritmo natural nos dois lados da equação:
Passo 2
Vamos usar o teste da primeira derivada para ver se é um máximo ou mínimo:
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um máximo relativo em .
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um mínimo relativo em .
E se tiver o mesmo sinal tanto em um intervalo aberto imediatamente à esquerda de quanto em um intervalo aberto imediatamente à direita de , então não tem extremo relativo em .
Vamos supor, , e :
Vamos então analisar as derivadas no intervalo que contém :
Pronto, temos então que e , então tem um máximo relativo em , então em temos a concentração máxima.
Passo 3
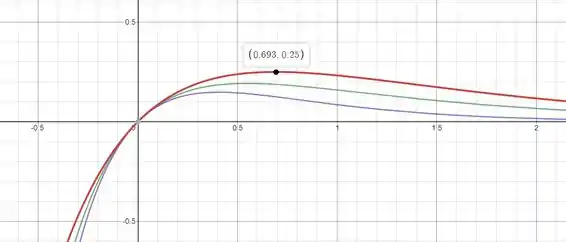
Pronto, pelo gráfico vemos que tem um máximo em .
