Se e forem números fixos, encontre equações paramétricas para a curva que consiste de todas as posições possíveis do ponto na figura, usando o ângulo como parâmetro. Então elimite o parâmetro e identifique a curva.
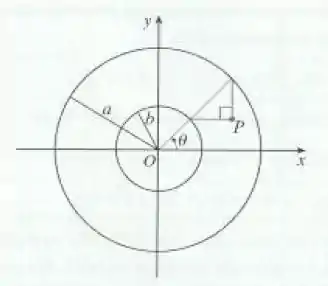
Passo 1
Queremos as coordenadas do ponto em função de , certo?
Vamos imaginar mais dois triângulos retângulos nessa figura, assim:
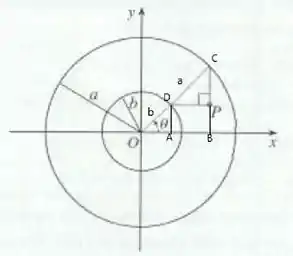
Então temos o triângulo menorzinho, que é o triângulo e o triangulo maior, que é o triangulo , beleza?
Se você reparar pela figura podemos dizer que as coordenadas do nosso ponto são
Só precisamos descobrir a medida desses segmentos e teremos a parametrização que queremos.
Passo 2
Como estamos falando de dois triângulos retângulos, podemos usar relações com seno e cosseno, assim, essas duas medidas saem rapidamente, olha só:
Do triangulo menor:
E do triangulo maior:
Isso significa que a parametrização da nossa curva é:
Passo 3
Agora precisamos eliminar o parâmetro e identificar que curva é essa em termos de e , ou seja, dizer a equação cartesiana dessa curva.
Bom, a ideia é a gente tentar isolar o parâmetro, mas como ele está associado a um seno e cosseno, vamos isolar o seno e o cosseno:
Agora o que que a gente usa toda vez que a gente quer se livrar de seno e cosseno?
Relação fundamental da trigonometria!!!!!
E isso é a equação de uma elipse.
Resposta
A curva é uma elipse.