Nos Exercicios de 1 a 36, faça um esboço do gráfico da equação dada
- (a)
Passo 1
Faala ae! Beleza? Aqui, vou esboço do gráfico da função utilizando o programa de computador geogebra.
Passo 2
Letra (a) Então! Aqui, temos que fazer o gráfico de uma reta com ângulo de inclinação . Ou seja, passando pela origem, é essa reta aqui:
O gráfico fica assim:
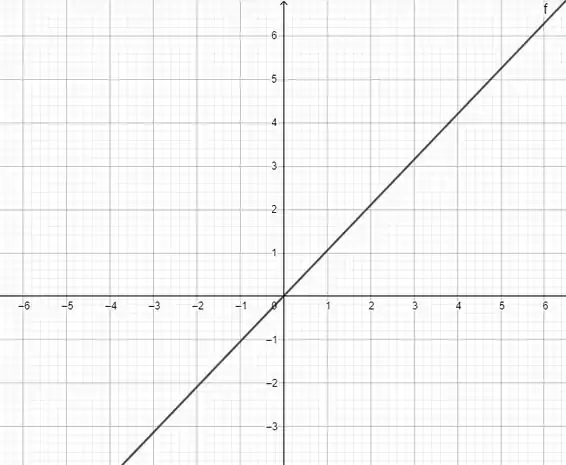
Passo 3
Letra (b) Dessa vez, vamos desenhar uma circunferência centrada na origem, com raio . Ou seja, seria essa equação:
O gráfico fica assim:
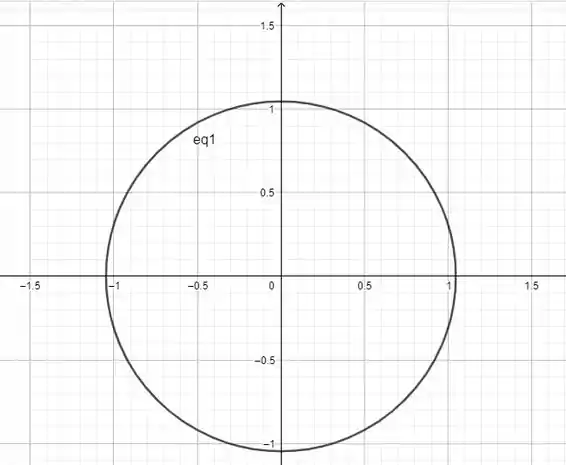
Resposta
Ei, a resposta está no passo a passo :)