Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 48

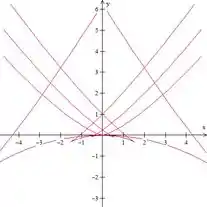
As curvas de catástrofe em forma de cauda de andorinha são definidas pelas equações paramétricas

Trace várias dessas curvas com o auxílio de uma ferramenta gráfica. Quais as características que essas curvas tem em comum? Como variam quando aumenta?

Passo 1

Bom, vamos determinar aqui alguns valores para e plotar, com o auxílio do Winplot as curvas resultantes pra ver o que podemos concluir.

Podemos definir e temos:

Podemos também fazer :

- :

Passo 2

Agora é só plotar todas essas curvas juntas no WinPlot, fazendo variar num intervalo razoável dentro dos reais, tipo, sei lá, de -10 até 10.

Temos isso daqui:

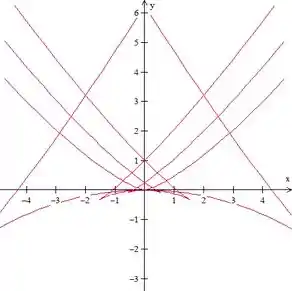
Quando temos temos algo que se assemelha a uma parábola que toca o ponto . Conforme aumentamos o valor de nossas curvas vão tomando o formato de cauda de andorinha e vao ficando cada vez maiores.

Resposta

Quando temos temos algo que se assemelha a uma parábola que toca o ponto . Conforme aumentamos o valor de nossas curvas vão tomando o formato de cauda de andorinha e vao ficando cada vez maiores.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use os gráficos de x = f ( t ) y = g ( t ) Para esboçar a curva paramétrica x = f ( t ) y = g ( t ) Indique com setas a direção na qual a curva é traçada à medida que t aumenta.

Encontre equações paramétricas para a elipse x 2 a 2 + y 2 b 2 = 1 Use as equações paramétricas para traçar a elipse quando a = 3 e b = 1 ,2 ,4e8 Como muda o formato da elipse quando b varia?

Mostre que as equações paramétricas x = x 1 + x 2 - x 1 t y = y 1 + y 2 - y 1 t Onde 0 ≤ t ≤ 1 descrevem o segmento de reta que une os pontos P 1 ( x 1 , y 1 ) e P 2 ( x 2 , y 2 ) .E encontre as equaç