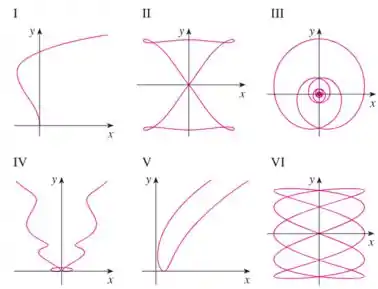
Associe as equações paramétricas aos gráficos . Dê razões para suas escolhas.
Passo 1
Falaee, belezinha??? Bom... o enunciado nos deu váias equações paramétricas, se liga:
E nos deu esses gráficos:
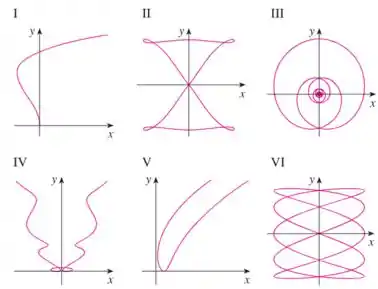
Queremos relacionar cada equação paramétrica com cada gráfico.
Para isso, vamos analisar cada equação e verificar o que acontece com e a cada aplicado.
Bora lá!! 😉
Passo 2
Aqui na letra (a), temos
Se , temos
Logo, vemos que o ponto inicial da curva ocorre em .
Com essa afirmação, já percebemos que a curva faz total sentido.
Mas vamos ver o que acontece no infinito?
Quando o temos que:
Logo, vemos que na curva tanto o quanto tende ao infinito positivo. Assim, podemos concluir que trata-se da curva .
Passo 3
Agora vamos analisar as equações da letra (b):
De forma análoga, vamos analisar de onde parte a curva quando :
E
Então a nossa curva parte da origem. Mas essa informação não tão relevante porque todas as curvas que sobraram parecem partir desse ponto haha.
Mas se liga: a gente já sabe que o não tá definido para valores negativos, pois é uma raiz.
Então só pode ser a opção ou .
Assim, nos resta analisar o comportamento da função no infinito:
Quando o temos que
E, dentre as curvas e , apenas a curva está tendendo para .
Passo 4
Analisando as equações da letra (c), temos:
Se fazemos , temos
E
Note que é periódica, com período igual a , então a interseção com o eixo só acontece quando , ou seja, quando:
Que por sua vez, só ocorre quando:
Ou
Logo, existem dois pontos na curva parametrizada em que a curva corta o eixo . Já sabemos que devemos procurar por uma curva com essa característica.
Além disso, pelas propriedades que vem lá da trigonometria, temos que:
E
Assim, nossa curva é tipo aquela parada de função ímpar, então podemos dizer que ela é simétrica em relação a origem.
E a curva é total simétrica em relação a origem e ela corta o eixo em dois pontos, além de passar pela origem. Beleza?
Passo 5
Analisando as equações da letra (d), temos:
Se temos
Além disso,
E o único gráfico que inclui o ponto e mantém e nesse intervalo é o gráfico da figura .
Passo 6
Analisando as equações da letra (e), temos:
Se fizermos temos o ponto
Sabemos que as funções seno e cosseno estão limitadas entre e para todo sempre na vida.
Das duas opções que nos restam, só uma está limitada entre e , que é a opção .
Acontece que aqui na letra (e), nossa curva tem um e um somados em cada uma das componentes.
Isso significa que se a gente fizer nossa curva vai tender a também.
E se fizermos o mas o . E a curva representa EXATAMENTE isso!
UHUUUUL!!
Passo 7
Por fim, analisando a letra (f), temos:
Se :
O único gráfico que passa por esse ponto é o gráfico da curva .