Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 51
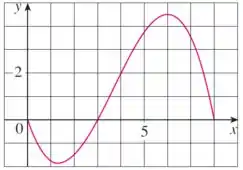
Para a função cujo gráfico é mostrado, liste as seguintes quantidades em ordem crescente, do menor ao maior e explique seu raciocínio.
Passo 1
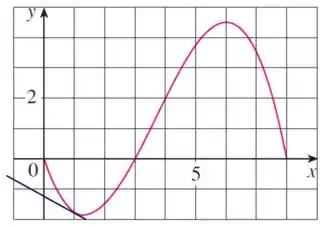
E aí, tudo certinho 😎? Nessa questão, sabemos que o gráfico de uma função desconhecida em um determinado intervalo é dado pela imagem abaixo.
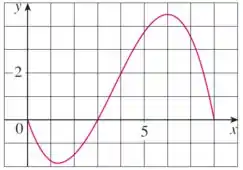
Com essa informação, precisamos listar em ordem crescente as cinco quantidades abaixo:
Parece que temos pouca informação, né? Mas tudo o que precisamos é lembrar que:
- O módulo da integral de uma função em um intervalo representa a área total entre a curva e o eixo , independentemente da curva estar acima ou abaixo do eixo.
- A integral definida será positiva se a curva da função estiver acima do eixo e negativa se estiver abaixo!
- A derivada representa a inclinação da reta tangente ao gráfico da função no ponto.
Além disso, repare que cada quadradinho na imagem tem lados medindo , logo, sua área é 1, beleza?
Com essas informações e com o auxílio do gráfico, vamos analisar cada uma das quantidades e colocá-las em ordem crescente. Bora lá 😊!
Passo 2
Vamos começar analisando as quantidades dadas pelas integrais definidas, combinado?
Bem, nas imagens abaixo destacamos as regiões delimitadas pela curva da função no intervalo e pelo eixo .
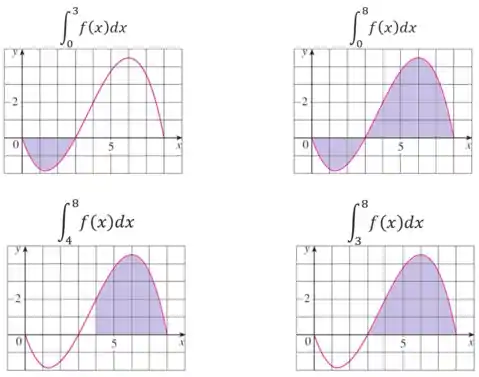
Observe que a quantidade dada por é negativa, pois a curva de está toda abaixo do eixo no intervalo
Além disso, as integrais e são positivas, pois a região pintada em ambos os casos está em cima do eixo .
Mas e a integral qual será o sinal dela?
Bem, apesar de termos uma região abaixo do eixo , a região que se encontra em cima aparenta ser muito maior, né? Você pode contar os quadradinhos também para confirmar!
Dessa forma, temos que:
e
Passo 3
Vamos agora ordenar as integrais positivas, beleza?
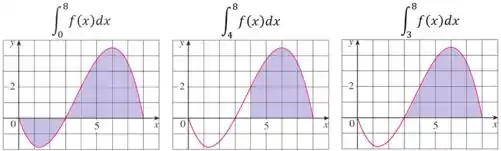
Agora, analisando as regiões assosicadas as integrais e conseguimos perceber que
pois a região pintada em é maior. De novo, você pode contar os quadradinhos para confirma 😊.
Além disso, observe que
então, como
vamos ter que
Sendo assim, para conseguirmos ordenar todas elas, só precisamos saber quem é menor:
Vamos usar os quadradinhos para nos ajudar 😆!
Na integral temos que um quadradinho de área foi removido da região entre a curva e o intervalo , ou seja,
Já na integral temos que
e podemos pensar que a área de toda região entre a curva no intervalo e o eixo , foi removida, já que é negativa. De fato,
pois tem mais de um quadradinho dentro da região e a curva está abaixo do eixo .
Dessa forma, vamos ter que
Ótimo!! Agora já conseguimos ordenar todas as integrais:
Falta só saber onde encaixar a quantidade , né? Vamos ver isso no próximo passo!
Passo 4
Como representa a inclinação da reta tangente ao gráfico da função no ponto então analisando a imagem abaixo percebemos que esse valor é negativo, devido a inclinação da reta.
Mas será que esse valor é maior ou menor do que
que vimos no passo anterior que satisfaz
De novo, vamos olhar para os quadradinhos =)!
Queremos avaliar a inclinação da reta tangente. Perceba que quando restringimos a reta a um quadradinho, a variação em é menor que a variação em , ou seja,
Porém, o módulo da inclinação da reta tangente em é exatamente essa variação, ou seja,
o que nos dá,
Pronto, como
então
Portanto, temos como resposta para a questão, a seguinte ordenação:
Resposta
Ordenando de maneira crescente as quantidades dadas, temos que: