Exercícios de Introdução e Definição de Integral - Lista de Exercícios Resolvida

Se , e , determine:

Analise as seguintes expressões:

Sabendo que elas são válidas e que , e são funções contínuas em , calcule os seguintes itens:

Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais.

Escreva como uma integral única na forma :

Considere o seguinte gráfico da função

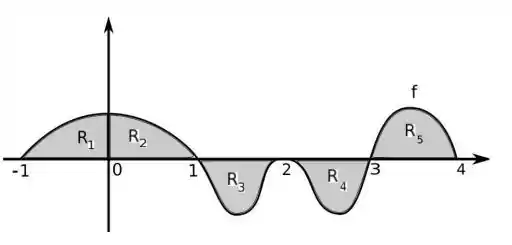
Sabendo que as áreas das regiões , , , e são:

.

Calcule:

Calcule a área da região limitada pela curva e abaixo das retas e .

O valor correto de é

se e se . Logo o menor valor possível de

É:

Decida se a proposição abaixo é falsa ou verdadeira, justificando:

Se e são integráveis, então:

Seja um polinômio quadrático tal que . O valor de é:

ME02) O valor de é

Q01II) Responda às perguntas abaixo no espaço adequado no seu caderno de respostas. As soluções devem ser sucintas e a resposta final deve estar destacada do restante da solução.

1. Se , é contínua e , quanto vale ?

Q02c) Calcule as seguintes integrais:

Calcule as integrais:

c)

Uma partícula se desloca sobre o eixo com uma função posição . Determine sabendo que:

Uma partícula se desloca sobre o eixo com uma função posição . Determine sabendo que:

Uma partícula se desloca sobre o eixo com uma função posição . Determine sabendo que:

Uma partícula se desloca sobre o eixo com uma função posição . Determine sabendo que:

Sejam um polinômio de grau estritamente menor que 3 e

Sabe-se que existe e é finito. E

e que

o valor de é:

Seja uma função. Explique primitiva, primitiva geral e integral indefinida usando e .

Encontre o comprimento do arco do gráfico da equação dada entre os ponto P e Q ou no intervalo especificado.

b)

Calcule a partir da definição as seguintes integrais:

a)

9.1. Verifique se a integral converge ou diverge. Caso seja convergente, calcule seu valor.

Seja . Um aluno propôs que a área limitada por e as retas , e é dada pela integral:

1. Calcule o valor numérico da integral .
2. A proposta do aluno está correta? Justifique.

Encontre o comprimento do arco do gráfico da equação dada entre os ponto P e Q ou no intervalo especificado.

a)

Calcule a partir da definição as seguintes integrais:

e)

Para a função dada abaixo, esboce seu gráfico e em seguida calcule .

Sejam e funções contínuas com:

Calcule as seguintes integrais:

Calcule a partir da definição as seguintes integrais:

f)

Calcule a partir da definição as seguintes integrais:

g)

Calcule a partir da definição as seguintes integrais:

d)

Calcule a integral.

02) Considere um circuito RC onde a força eletromotriz é alternada, de modo que , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.

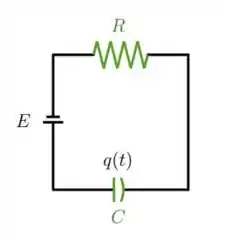
a) Mostre que a carga satisfaz uma equação da forma .

Para os próximos itens considere que .

b) Encontre uma primitiva de e determine e também .

c) Obtenha a solução geral da equação determinada no primeiro item.

d) Determine a solução com carga inicial . Mostre que , mostrando que esse limite não depende da carga inicial .

Seja uma função cuja derivada é . Explique primitiva, primitiva geral e integral indefinida usando e .

Calcule a partir da definição as seguintes integrais:

b)

4. Calcule a integral ou mostre que ela e divergente.

Seja a área da região sob o gráfico , acima do eixo , entre as retas e . Selecione a alternativa que apresenta uma forma correta de obter o valor de como limite de somas de áreas de retângulos.

Calcule a derivada da função dada por:

Uma partícula se desloca sobre o eixo com uma função posição . Determine sabendo que:

Calcule a partir da definição as seguintes integrais:

c)