Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 10
Uma função é dada por uma tabela de valores, um gráfico, uma fórmula ou por meio de descrição verbal. Determine se é injetora.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar se é injetora.
Pra isso, temos que lembrar que uma função é chamada injetora quando ela não assume o mesmo valor duas vezes; isto é:
sempre que
Então, vamos analisar o comportamento da nossa função e verificar se para cada valor de existe um valor de diferente.
Vamos lá!
Passo 2
A função é uma parábola, portanto é simétrica a uma reta paralela ao eixo . Olha só:
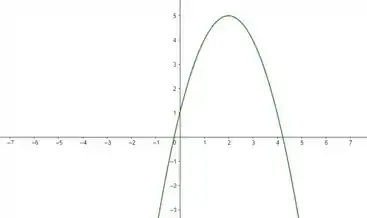
Isso quer dizer que a função possui pontos em que , ou seja, existem valores iguais de para diferentes valores de . Portanto, essa função não é injetora.
Valeu, galera! Até a próxima! 😉