Nos Exercícios de 1 a 18, determine se a função é biunívoca. Faça um esboço do gráfico da função.
16.
Passo 1
Primeiro vamos entender o que é uma função biunívoca (ou injetora). Uma função dessa forma tem a característica de que cada componente do seu domínio só tem um correspondente em sua imagem. O diagrama a seguir demonstra essa característica.
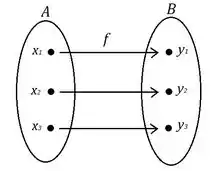
Onde A é o domínio da função e B é a imagem dessa função, pode – se reparar que cada membro do domínio corresponde a um único membro da imagem.
Passo 2
Entendendo o que o passo 1 nos diz, é possível ver logo de cara que essa função não é biunívoca já que qualquer valor que você pegue para x a função sempre vai nos dar o mesmo valor 5.
Assim, todo ponto do domínio tem o mesmo valor na imagem.
Passo 3
Agora vamos ver como ficaria o gráfico dessa função.
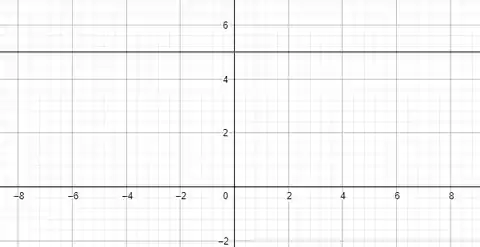
Através do gráfico também é possível ver o que constatamos no passo 2.
Resposta
A função não é biunívoca.