Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.1 - Ex. 19
Nos exercícios de 19 a 40, determine se a função dada tem uma inversa. Se a inversa existir, determine – a e faça o seguinte: (a) ache o domínio e a imagem; (b) faça esboços dos gráficos da função e de sua inversa, no mesmo conjunto de eixos. Se a função não tiver uma inversa, mostre que uma reta horizontal intercepta o gráfico da função em mais de um ponto.
19.
Passo 1
Para saber se uma função tem inversa, basta verificar se a função biunívoca.
Então temos que verificar se nossa função biunívoca.
Para fazer isso, vamos usar o teorema 7.1.2 do capítulo 7, seção 2, que diz que se uma função for crescente ou decrescente em todo seu domínio ou intervalo, ela é biunívoca.
Para saber se a função é crescente ou decrescente vamos derivar a função e ver se ela é negativa no seu domínio ou positiva.
Passo 2
Vamos derivar a função.
Como a função para todo podemos concluir que é crescente.
Assim, a função não assume os mesmos valores na imagem com o mesmo elemento do domínio, logo ela é biunívoca, logo admite inversa.
Passo 3
Agora vamos achar função inversa.
Tendo:
Passo 4
Tendo a inversa da função definida como:
Podemos ver que ela não tem nenhuma restrição para um valor de y, logo o domínio da função inversa que é a imagem da função normal está contido no conjunto dos números reais. A imagem da função inversa é o domínio da função normal, logo sua imagem está contida no conjunto dos números reais.
Passo 5
Agora vamos ver como fica o gráfico das duas funções.
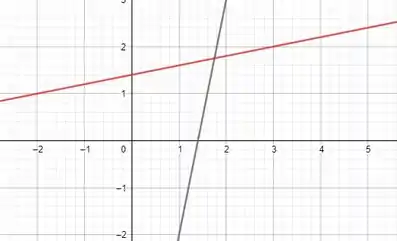
A reta cinza representa e a reta vermelha representa .
Resposta
Ei, a resposta está no passo a passo :)