Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 72
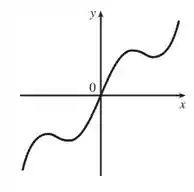
Uma função tem o domínio e é mostrada uma parte do seu gráfico.
a) Complete o gráfico de sabendo que é uma função par.
b) Complete o gráfico de sabendo que é uma função ímpar.
Passo 1
E aí, pessoal! 😊
Nesse problema foi dada um gráfico de uma função contida apenas no primeiro quadrante e nosso objetivo é esboçar o gráfico dessa função caso essa função seja (a) uma função par e (b) uma função par.
Lembra como fazemos isso? 😉
Uma função é chamada de par quando o seu gráfico é simétrico em relação ao eixo vertical (eixo ).
Isso significa que, para qualquer valor de , a função assume o mesmo valor para e para . Em outras palavras, para todo no domínio da função.
Um exemplo de função par é a função quadrática , cujo gráfico é uma parábola que se abre para cima e é simétrica em relação ao eixo .
Uma função é chamada de ímpar quando o seu gráfico é simétrico em relação à origem (ponto ).
Isso significa que, para qualquer valor de , a função assume o valor oposto para e para . Em outras palavras, para todo no domínio da função.
Um exemplo de função ímpar é a função linear , cujo gráfico é uma reta que passa pela origem e é simétrica em relação a ela.
Sacou? Bora lá! 😬
Passo 2
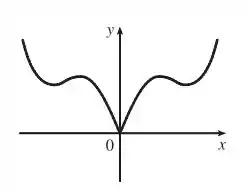
Como é uma função par, nós apenas a refletimos em torno do eixo , obtendo o seguinte gráfico:
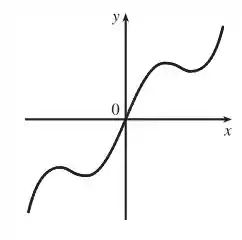
sendo uma função ímpar, construímos seu gráfico primeiro girando em torno do eixo , como no gráfico acima, depois refletindo ela para baixo, girando , obtendo a seguinte figura:
E aí! Entendeu tudo? Responde Aí! 😉
Resposta
Par:
Ímpar:
