Exercícios de Funções Pares e Ímpares - Lista de Exercícios Resolvida
Questão 1
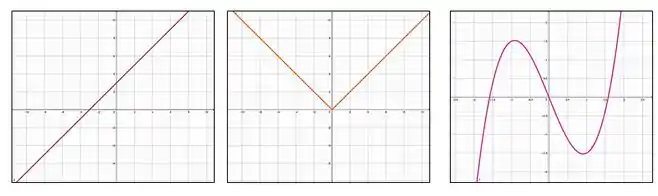
Classifique as funções abaixo em pares, ímpares ou sem paridade.
- b) c)
Questão 2
Considere a afirmação a seguir:
A função possui um gráfico simétrico ao eixo y. A afirmação está:
a) Correta, pois a função é par
b) Correta, pois a função é ímpar
c) Falsa, pois a função é ímpar
d) Falsa, pois a função não possui paridade
e) Não tem como saber
Ver solução completaQuestão 3
- Verifique a paridade da função :
- Calcule :
- Verifique a paridade da função .
Ver solução completaQuestão 6
Seja a função
Podemos afirmar que f é uma função:
( ) Ímpar
( ) Par.
( ) Dependendo dos valores de x f pode ser par ou impar
( )É par e impar simultâneamente
( )Nem é par,nem impar
Ver solução completaQuestão 7
Seja .
Verifique se a função é par, ímpar ou injetora. Justifique sua resposta provando ou dando contraexemplo.
Ver solução completaQuestão 9
Determine se cada afirmativa abaixo é sempre verdadeira, ou pode ser falsa. Justifique sua resposta.
- O produto de uma função ímpar por uma função par é uma função par.
Questão 10
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
42.
Ver solução completaQuestão 11
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
45.
Ver solução completaQuestão 12
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
44.
Ver solução completaQuestão 13
- Considere a dada por e suas derivadas e
- Identique os intervalos em que essa função é positiva, negativa e determine os seus zeros (raízes). Determine se ela exibe simetrias.
Ver solução completaQuestão 14
Sejam f uma função definida em R. Mostre que as funções
e
são funções, respectivamente, par e ímpar. Em seguida, mostre que toda função com domínio R pode ser escrita com soma de uma função par com uma função ímpar.
Ver solução completaQuestão 15
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
41.
Ver solução completaQuestão 16
Nos exercícios 31 a 46 esboce o gráfico da função, especificando o domínio, a imagem e, quando possível, a paridade (par ou ímpar).
40.
Ver solução completaQuestão 17
Sejam e , (a) verifique se as funções dadas são pares, ímpares, ou nenhuma das alternativas, (b) encontre o domínio de e .
Ver solução completaQuestão 18
9. Se é uma função ímpar e periódica com período igual a , então é igual a.
Questão 19
4. Seja uma função períodica. Considere as quatro seguintes afirmações:
- não é par.
- é impar.
- não é bijetora.
- Para um dada , a equação ou não possui solução ou possui infinitas soluções.
São corretas:
- Somente
- Somente
- Somente
- Todas
- Somente