Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 37
Investigue a família de curvas dadas por , em que é um número real. Comece calculando os limites quando . Identifique qualquer valor intermediário de onde mude a forma básica. O que acontece aos pontos de máximo, de mínimo e de inflexão quando varia? Ilustre fazendo o gráfico de vários membros da família.
Passo 1
Oieee, bora resolver mais uma comigo??
Vamos resolver a questão passo a passo.
Limite quando tende a
Para calcular o limite quando tende a , basta observar que a função exponencial domina a função para grande o suficiente.
Portanto, para qualquer valor de
Identificação de mudanças na forma básica para valores intermediários de
A forma básica da função é determinada principalmente pelo valor de
Quando a função se torna uma reta. Conforme aumenta, a função exponencial domina mais rapidamente, fazendo com que a curva se aplane mais rapidamente.
Quando é pequeno, a função é quase uma reta.
Conforme aumenta, a curva se torna mais inclinada em direção ao eixo negativo.
Quando é muito grande, a função se aproxima de
Passo 2
Comportamento dos pontos de máximo, mínimo e inflexão quando varia:
- Pontos de Máximo e Mínimo: Para encontrar os pontos de máximo e mínimo, podemos derivar a função em relação a e igualar a zero para encontrar os pontos críticos.
A função é diferençável em todos os valores de então podemos usar a primeira derivada para encontrar os pontos críticos. Derivando em relação a obtemos:
Igualando isso a zero e resolvendo para obtemos os pontos críticos.
No entanto, para simplificar, podemos perceber que nunca será zero para real.
Portanto, a única solução para é quando o segundo termo se anula, ou seja, quando
Isso nos dá um ponto crítico em
Passo 3
Para determinar se este ponto é um máximo ou um mínimo, podemos usar o teste da segunda derivada. A segunda derivada de é:
Avaliando em , obtemos:
Se então
O que indica um ponto de máximo.
Se então
Passo 4
Indicando um ponto de mínimo.
- Pontos de Inflexão: Para encontrar os pontos de inflexão, precisamos encontrar onde a concavidade da curva muda.
Isso ocorre quando a segunda derivada muda de sinal.
No entanto, como a segunda derivada já é negativa em , não haverá pontos de inflexão nesta função.
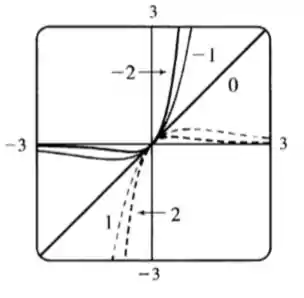
Gráfico de vários membros da família:
Podemos traçar vários membros da família de curvas para diferentes valores de para visualizar melhor como a forma da curva muda. Por exemplo, podemos traçar para
Isso nos ajudará a entender como a inclinação da curva muda com
Resposta
Vide o passo a passo.