Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.5 - Ex. 94
- Se é contínua, mostre que
- Use a parte (a) para calcular e .
Passo 1
Opa, bora resolver esse problema! Na letra (a) temos que demonstrar que:
Se a gente reparar, a função e tem uma defasagem de :
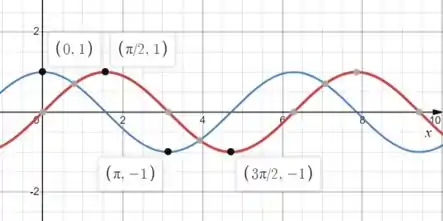
Essa curva de azul é e a de vermelho é . Então podemos usar a substituição:
Então podemos dizer que:
Isso significa que o valor de é o mesmo que o valor de de um ângulo complementar a
Assim:
E para resolver essa integral temos que aplicar a regra da substituição:
Então temos que a regra deve ser realmente o inverso da regra da cadeia. De acordo com a regra da cadeia para a derivada temos:
Na integração por substituição, pegamos uma expressão da forma e encontramos sua primitiva.
A integração por substituição nos ajuda a simplificar uma expressão confusa, transformando a função "interna" na variável. Então temos que encontrar o resultado dessa integral:
Para simplificar essa integral, colocamos uma nova variável tal que . Isso significa que .
Também precisamos alterar os limites de integração, e para isso é só avaliar o valor de para ambos os limites!
Substituindo essas expressões na integral, obtemos:
A integral agora é muito mais simples de resolver, pois é uma função direta de . Após integrar em relação a , obtemos .
Finalmente usamos o TFC (Teorema Fundamental do Cálculo) para avaliar os limites de integração, ou seja:
Ah! Detalhe que vamos ter que aplicar a regra da substituição em ambas os itens, (a) e (b)!
Para o item (b) vamos precisar usar as seguintes identidades trigonométricas:
E a integral da função cosseno:
Passo 2
Vamos calcular a integral da esquerda para tentar chegar em:
Assim provamos a igualdade do enunciado.
Vamos a nossa integral:
Podemos fazer a substituição (lembra que ela tem que ser algo que facilite a nossa vida!), logo vamos chamar de:
Calculando a sua derivada, e isolando :
Também precisamos alterar os limites de integração:
Substituindo tudo na nossa nova integral:
Vamos aplicar a propriedade que uma integral multiplicada por altera seus limites de integração:
Podemos dizer que:
Temos enfim:
Aweeee!!!
Passo 3
Agora a letra (b)! Devemos usar a parte (a) para calcular
e
Teremos que , então:
E
Vamos provar que as duas chegaram ao mesmo resultado, logo:
Vamos começar com a
Podemos reescreva usando a identidade trigonométrica como:
Primeiramente vamos aplicar a propriedade que a integral da soma é a soma das integrais:
A da esquerda é moleza, mas e a da direita? E como resolver essa nova integral? Substituição novamente!
Vamos chamar de :
Derivando para encontra o :
Isolando :
Agora os limites de integração:
Vamos montar nossas integrais:
Agora resolvendo separadamente:
Para essa usamos a primitiva constante e avaliamos para os limites:
Agora a segunda derivada, tirando o que é constante multiplicativa para fora para facilitar nossos cálculos:
Juntando tudo até aqui:
Agora precisamos fazer tudo isso para encontrar a do seno?? Nãaaao, ufaaa!
Vamos usar a seguinte propriedade:
Vamos integrar toda essa expressão?
A integral de é a integral da constante:
Também acabamos de calcular a integra da função cosseno ao quadrado, substituindo tudo o que temos:
Isolando a integral:
Chegamos enfim:
Prontinho!
Resposta
- Demonstração