Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 6
O gráfico da derivada de uma função é mostrado.
- Em que intervalo é crescente ou decrescente?
- Em que valores de , tem um máximo local ou mínimo?
Passo 1
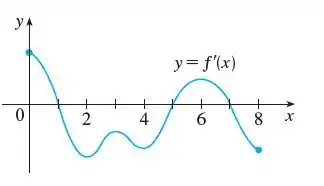
E aíii, tudo bom?! Nesse probleminha temos o gráfico de :
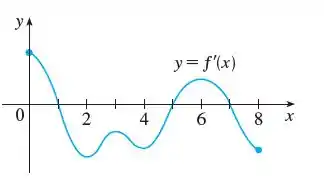
E o enunciado nos pede duas coisas:
- Na letra (a) devemos apontar os intervalos onde é crescente ou decrescente;
- Na letra (b) temos que encontrar os valores de onde é um ponto de máximo ou mínimo da função .
Essa é uma questão de análise de gráfico, então ela é bem direta, mas temos que ter em mente algumas informações sobre derivadas!
- Se então é crescente;
- Se então é decrescente;
- Se , esse é um ponto crítico, que pode ser um máximo ou mínimo.
Beleza, mas como eu sei se o ponto é máximo ou mínimo?!
Muito simples, em um ponto de máximo primeiro a função cresce, chega ao máximo e depois decresce, então se:
- positivo negativo: Temos um ponto de máximo local;
- negativo positivo: Temos um ponto de mínimo local;
Agora vamos colocar a mão na massa!
Passo 2
Na letra (a) vamos analisar os intervalos de crescimento e decrescimento de , pra isso vamos trazer o gráfico pra pertinho:
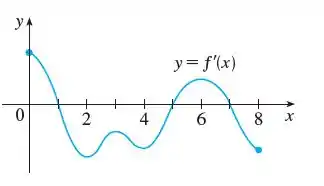
Lembrando que é crescente quando , olhando o gráfico temos então que é crescente nos intervalos:
e
é decrescente quando , olhando o gráfico temos então que é decrescente nos intervalos:
e
Bem simples, agora a letra (b)!
Passo 3
De novo, vamos trazer o gráfico pra pertinho:
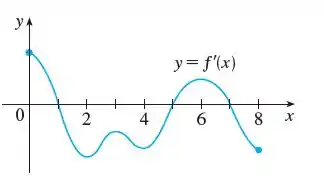
tem um valor máximo local quando troca de sinal de positivo para negativo, vemos no gráfico que isso ocorre em:
e
E tem um valor mínimo local quando troca de sinal negativo para positivo, vemos no gráfico que isso ocorre em:
Prontinho!
Resposta
- é crescente em e , e decrescente em e
- tem um valor máximo local em e , e mínimo local em