Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.11 - Ex. 3
O gráfico indica como a população da Austrália está envelhecendo, apontando o passado e a porcentagem projetada da população com idade superior ou igual a 65 anos. Use uma aproximação linear para prever a porcentagem da população que terá 65 anos ou mais nos anos 2040 e 2050. Você acredita que suas previsões estão muito para mais ou para menos? Por quê?
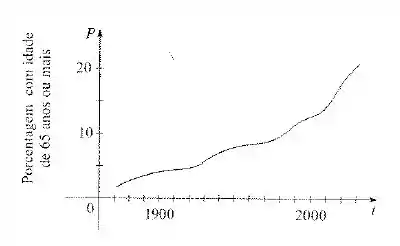
Passo 1
Queremos estimar o valor de para os anos de 2030 e 2040, e faremos isso usando uma linearização da função usando como base a função no ano de 2030. A linearização da função , utilizando como base o ano 2030, pode ser feita da seguinte maneira:
Devemos então obter do gráfico o valor da função para e também uma estimativa do valor da derivada de em relação a nesse ponto.
Passo 2
Primeiro vamos obter através do gráfico :
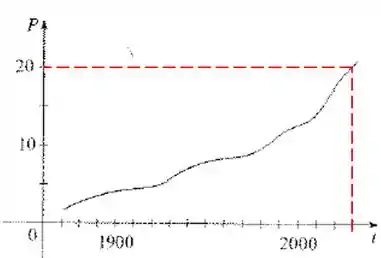
Podemos ver na imagem que:
Agora vamos estimar o valor da derivada. Fazemos isso traçando uma tangente à curva no ponto e calculando a tangente do seu ângulo de inclinação:
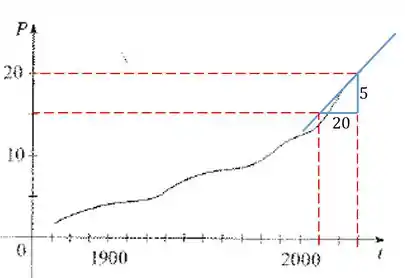
Passo 3
Agora que temos e , podemos aplicar o ajuste linear para os anos de 2040 e 2050:
A curva está abaixo da reta tangente onde fizemos a aproximação, então os valores de para os anos de 2040 e 2050 são na verdade menores do que os que calculamos.
Resposta
Valores superestimados.