Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 52
Investigue, com o auxílio de uma ferramenta gráfica, a família de curvas definidas pelas equações paramétricas
Comece tomando como um inteiro positivo e veja o que acontece com a forma à medida que cresce. A seguir, explore algumas das possibilidades que ocorrem quando é uma fração.
Passo 1
Oie, tudo bem? Vou te ajudar a resolver essa atividade hoje.
Aqui é uma atividade onde deveremos utilizar um software gráfico.
A gente vai investigar o comportamento da família de curvas:
Bom, para resolver essa atividade iremos colocar diversos valores para e observar o que é gerado com o auxilio do winplot. Veja que você pode também utilizar o GeoGebra ou o Desmos, o resultado será o mesmo.
Passo 2
Primeiro vamos fazer só valores inteiros e maiores que zero pra .
Começando com :
Ficamos com uma reta com :
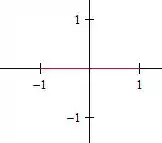
Agora :
E ai o negócio já deu uma enrolada doida:
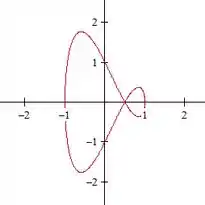
Agora :
Enrolou duas vezes agora:
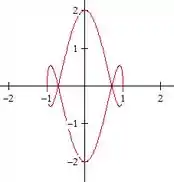
E :
Enrolou mais uma vez, fazendo uma bolinha pequena ali no meio:
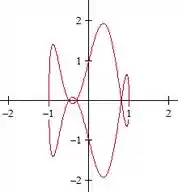
Vamos testar :
Enrolou mais uma vez:
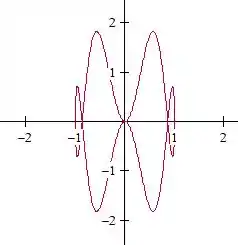
Acho que já mais do que deu pra perceber que conforme aumenta, sendo e inteiro, nossa curva oscila (ou enrola) mais.
E você pode perceber que para valores impares de ela se torna simétrica em relação ao eixo .
Passo 3
Agora vamos testar valores para de modo que seja uma fração, mas ainda maiores do que zero.
Por exemplo,
E temos um ovinho:
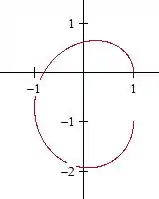
Agora :
E temos um ovinho um pouco menor:
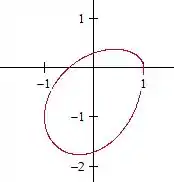
Agora :
O ovinho deu um laço:
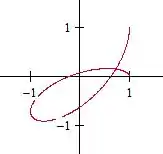
Agora vamos fazer um :
E aí fica assim:
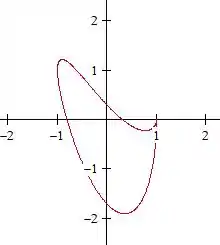
Olha, tá me parecendo que para fracionário nossa curva não tá muito seguindo um padrão não...
Resposta
A medida que inteiro positivo cresce, o o número de oscilações da curva aumenta. Já a medida que fracionário varia, a curva não varia num padrão.