Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 46
Se um projétil for atirado com uma velocidade inicial metros por segundo com um ângulo acima da horizontal e a resistência do ar for considerada desprezível, então sua posição, depois de segundos é dada pelas equações paramétricas
Onde é a aceleração da gravidade .
- Se uma arma foir disparada com e , quando a bala atingirá o solo? A que distância da arma a bala atingirá o solo? Qual altura máxima alcançada pela bala?
- Use um dispositivo gráfico para verificar suas respostas na parte (a). Em seguida, faça um gráfico da trajetória do projétil para vários outros valores do ângulo para ver onde ele atinge o solo. Resuma suas descobertas.
- Mostre que a trajetória é parabólica eliminando o parâmetro.
Passo 1
Oiii, tudo certinho contigo?? Vamos resolver mais uma questãozinha??
O enunciado nos dá as equações da posição de um objeto que foi atirado num lançamento oblíquo:
Onde é a trajetória na horizontal e , da vertical.
Além disso, é a velocidade inicial, é o ângulo que o abjeto faz com a horizontal, é o tempo, é a aceleração da gravidade.
Na letra (a) queremos encontrar o tempo e a distância em que a bala atingirá o solo quando e . Além disso, também queremos encontrar a altura máxima.
Para isso, sabemos que a bala atingirá o solo quando a altura for zero. Assim, a gente encontra o valor de e aplica em .
Sabemos também que a altura máxima ocorre na metade do tempo. Assim, a gente substituir o novo valor de em para encontrar a altura máxima.
Em seguida a gente plota o gráfico de para confirmar esses valores. E, por fim, isolamos em uma das equações e substituímos na outra para verificarmos que a trajetória é parabólica (uma equação do segundo grau).
Agora bora lá!! 😉
Passo 2
Com os dados que ele deu pra gente aqui na letra a), temos que as equações paramétricas da trajetória da bala é dada por
E
Como ele quer saber quando a bala atingirá o solo, basta que a gente faça e assim teremos o valor do instante em que ela cai no chão, sacou?
ou
Assim, o instante em que a bala atingirá o solo novamente é .
Passo 3
Agora para saber a que distância da arma a bala cai no chão, vamos considerar que a arma está na origem dos eixos.
Dessa forma, a distancia da bala até a arma é dada por e para descobrir essa distância basta substituir na parametrização de .
Assim, a bala caiu a uma distancia de mais ou menos da arma.
Passo 4
Agora para encontrar a altura máxima atingida pela bala, a gente pensa o seguinte, se ela leva segundos para cair no chão novamente, então na metade desse tempo ela estava lá na altura máxima que ela atingiu.
Faz sentido?
Assim, o tempo para ela atingir a altura máxima é
(você poderia chegar a essa conclusão também pegando a componente , derivando e igualando a zero).
E a altura máxima é:
Ou seja, a bala atinge uma altura máxima de aproximadamente .
Passo 5
Vamos para letra (b) agora.
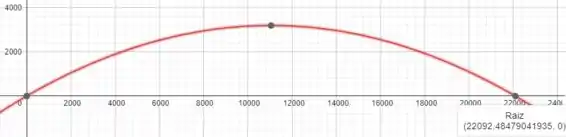
Plotando essas equações paramétricas, observamos o seguinte gráfico:
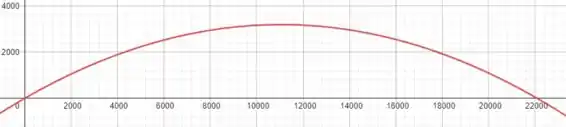
Note que já respondemos a letra (c) aqui rsrs (mas a gente vai demonstrar ela no passo 6 😉)
Agora, analisando o gráfico, podemos analisar que o ponto de máximo ocorre mesmo em , que foi o valor calculado:
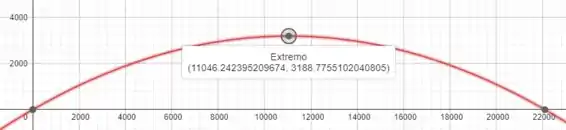
Também a gente pode ver a distância total:
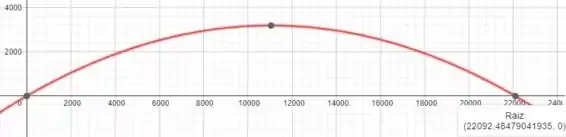
Note que a distância total foi igual a calculada, ou seja, .
Passo 6
Agora vamos ver o que acontece quando mudamos o ângulo para ver onde o projétil atinge o solo.
Aqui é o seguinte: A altura máxima e a maior distância alcançada ocorrem quando a velocidade inicial do objeto é dividida igualmente entre as componentes horizontal e vertical do movimento.
Assim, o lançamento vai ter maior altura e maior distância quando lançados em um ângulo de !!
Passo 7
Agora vamos eliminar o parâmetro para mostrar que se trata de uma parábola.
Nossa parametrização é:
Isolando na primeira equação, temos:
Substituindo na segunda:
Que nada mais é que a equação de uma parábola
Resposta
(a)
O instante em que a bala atingirá o solo novamente é .
A bala caiu a uma distancia de mais ou menos da arma.
A bala atinge uma altura máxima de aproximadamente .
(b)
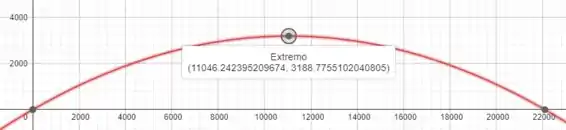
O lançamento vai ter maior altura e maior distância quando lançados em um ângulo de .
(c)