Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 47
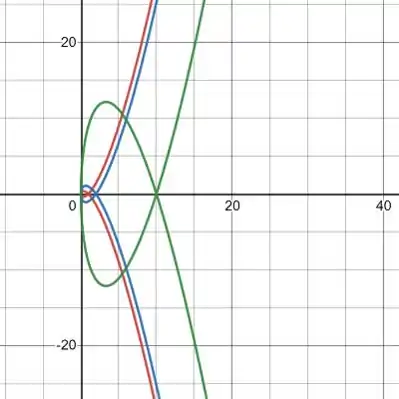
Investigue a família de curvas definidas pelas equações paramétricas
Como muda o formato quando aumenta? Ilustre traçando vários membros da família com o auxílio de uma ferramenta gráfica.
Passo 1
Olá, meu grande amigo. Sei que parece que essa atividade é extremamente difícil, mas irei te ajudar a resolvê-la e você perceberá que não.
A gente tem a curva parametrizada:
E a gente vai investigar as famílias de curvas que possuem essa equação paramétrica. No caso, iremos investigar o termo:
Pois ele tem a constante , que podemos mudar e obter diferentes tipos de curvas. Para trabalhar nessa questão, vamos utilizar o GeoGebra, ele irá nos ajudar a visualizar o comportamento da nossa curva paramétrica.
Outra coisa que a gente pode fazer, é colocar a equação em coordenadas cartesianas, isso é, iremos isolar e colocar ele na outra equação, tendo assim apenas uma função dependente de .
Passo 2
Bom, vamos tentar fazer o valor de variar e ver as curvas que temos:
Começando com
Vamos isolar o na primeira equação para substituir na segunda e encontrar a equação cartesiana dessa curva para podermos plotar.
Substituindo na equação do :
Plotando isso com uma ferramenta gráfica, temos:
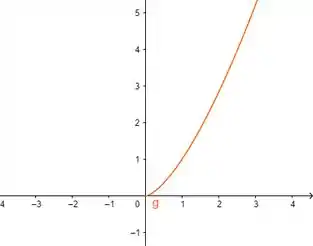
Passo 3
Agora vamos fazer , por exemplo, :
Isolando na primeira equação:
Substituindo na equação do :
Plotando isso, com auxílio de uma ferramenta gráfica:
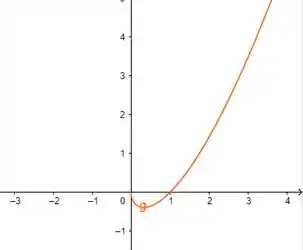
Passo 4
Vamos continuar com , porém em vez de pular para , vamos para um valor de maior, para vermos se tem alguma diferença significativa. Por exemplo, .
Substituindo na equação do :
Plotando isso, com auxílio de uma ferramenta gráfica:
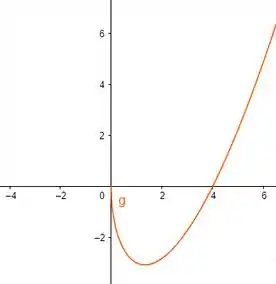
Vemos que o que acontece é que a barriguinha do gráfico fica bem maior. Então a medida que aumentamos nosso , a “barriga” do gráfico aumenta.
Passo 5
Agora vamos tentar , começando com :
Isolando na primeira equação:
Substituindo na equação do :
Plotando isso, com auxílio de uma ferramenta gráfica:
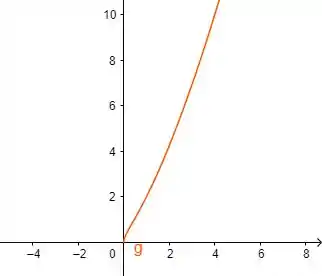
Repara que o gráfico ficou semelhante com o primeiro gráfico, só que um pouco mais retilíneo.
Passo 6
Continuando com , agora vamos testar :
Substituindo na equação do :
Plotando isso, com auxílio de uma ferramenta gráfica:
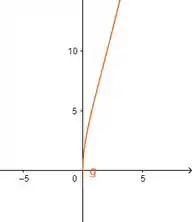
Mais retilíneo ainda!
Passo 7
Agora, antes de plotarmos todas as curvas juntas, vamos pensar o seguinte.
Como desenhamos nossas curvas a partir das equações cartesianas que elas representam, nossas curvas estão amarradas à imagem das funções cartesianas. Que não necessariamente são as imagens das curvas.
A questão não deixou claro, mas vamos assumir que o parâmetro das curvas possa valer qualquer coisa, ou seja, . Dessa forma, o que a gente desenhou aí foi só metade das nossas curvas, representadas por essas funções.
Mas a curva mesmo é o dobro disso, ou seja, ainda temos que rebater o que tá desenhado aí em relação ao eixo . (não pode ser em relação ao eixo porque nossas funções nem estão definidas para ).
Aí plotando tudo junto e rebatendo a gente fica com um negócio meio lokao assim:
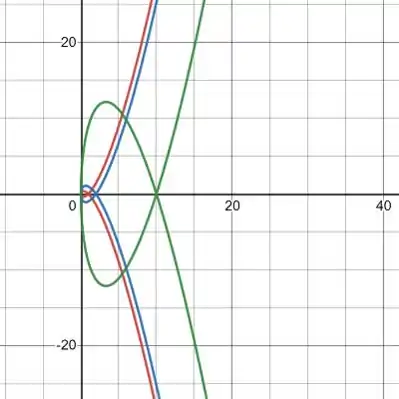
Resposta
