Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 23
Trace a curva em uma janela retangular que mostre todos os aspectos importantes da curva
Passo 1
Pra começar, WTF de questão é essa???
Como assim todos os aspectos importantes da curva? Custava dizer o que ela queria???
Bom, enfim, mas vamos entender que ela considera como importante que a gente mostre pontos em que a reta tangente da curva é horizontal e vertical.
E já que a questão não deixa muito claro como ela quer que a gente faça isso, vamos calcular os pontos em que a curva tem retas tangentes horizontais e verticais e depois a gente plota nossa curva de modo a mostrar esses pontos, beleza?
Passo 2
Vamos começar pelos pontos onde nossa reta tangente é horizontal.
Isso ocorre quando
Então, vamos fazer aquela mesma ladainha de sempre: achar essa derivada, igualar a zero para encontrar o valor de em que isso ocorre e depois substituir na parametrização da curva para encontrar o ponto correspondente.
Passo 3
Passo 4
Substituindo na parametrização da curva, temos:
Portanto, a reta tangente é horizontal nos pontos
Passo 5
Agora vamos ver os pontos onde a reta tangente é vertical.
Assim,
Passo 6
Substituindo na parametrização da curva, temos:
Substituindo na parametrização da curva, temos:
Substituindo na parametrização da curva, temos:
Portanto, a reta tangente é vertical nos pontos
Passo 7
Show, agora a gente tem que plotar a nossa curva num gráfico que mostre todos esses pontos.
Para isso, precisamos que o intervalo de variação do nosso parâmetro abranja os valores de para os quais a curva tem retas tangentes horizontais e verticais.
Esses valores de são
O menor valor de todos é
E o maior valor de todos é
Então vamos fazer um gráfico com
Pra termos uma folguinha...
PS: não fica chateado comigo por ter calculado os pontos exatos onde as retas tangentes horizontais e verticais ocorrem. A gente não precisava necessariamente ter feito isso, mas é bom ter feito pra você poder olhar no gráfico agora e confirmar que nesses pontos de fato tem retas tangentes horizontais e verticais.
Passo 8
Tá, agora vamos plotar nossa curva:
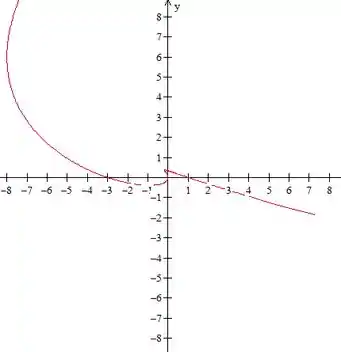
Essa janela aí acabou sendo uma janela quadrada . Mas podemos dar um zoom nisso pra vc conseguir ver melhor os outros pontos também.
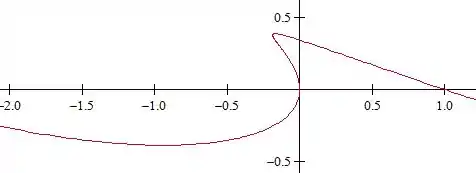
E agora ficamos com uma janela retangular que você consegue ver aqueles pontos que eram menores mais de pertinho.
Resposta
Ei, a resposta está no passo a passo :)