Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 10.1 - Ex. 18
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Eaee, belezinha?? Bom... o enunciado as seguintes equações:
Queremos primeiro eliminar o seno e cosseno hiperbólicos para encontrar uma equação cartesiana da curva.
Para isso, precisamos saber da seguinte relação:
Em seguida, devemos esboçar a curva e indicar com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Agora bora lá!! 😉
Passo 2
Vamos reescrever nossas equações isolando o seno e cosseno hiperbólicos:
E
Para “isolar” o parâmetro no caso em que temos seno hiperbólico e cosseno hiperbólico, usamos a relação fundamental da trigonometria:
Assim
Que é a equação de uma hipérbole, “olhando” para o eixo , que é a variável que tá com sinal negativo.
Agora vamos analisar o que fizemos!!
Passo 3
Perceba que, para qualquer valor de :
E que também, temos que:
“Juntando” essas duas informações, podemos concluir que para nossa equação:
Assim, estamos falando do ramo da hipérbole que está na parte positiva do eixo , com foco no ponto .
Passo 4
Traçando nossa curva e percebendo que o parâmetro aumenta para , temos:
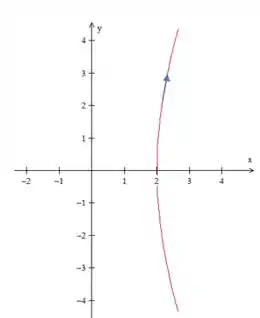
Resposta
a)
b)
