Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 72
Para o limite
Ilustre a Definição 7 encontrando os valores de que corresponde a e
Passo 1
Fala aí! como vai?
Nesse problema foi dado o limite
E nosso objetivo é aplicar a Definição e encontrar os valores de que correspondem a e .
Tem ideia de como fazemos isso?
Bom pessoal, vamos ver o que diz a Definição 7:
Seja uma função definida em um intervalo Então:
Significa que para todo existe um numero N correspondente tal qual:
Sacou? Vamos aplicar no nosso problema!
Passo 2
Então nós vamos fazer o caminho contrário. Temos a seguinte relação:
Com , logo
Tirando o módulo, ficamos com:
Agora s�� substituir ...
Para , temos a relação:
Então
Plotando o gráfico da função com o auxílio de uma ferramenta gráfica, podemos ver quais valores de correspondem aos achados acima.
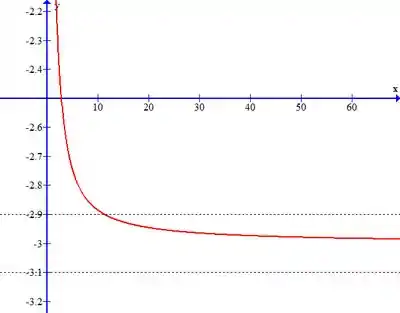
Para .
Então, podemos estabelecer um número imediatamente maior:
Deste modo, para qualquer:
Tranquilo até aqui?
Passo 3
Para , faremos a mesma coisa:
Então
Plotando o gráfico da função com uma ferramenta gráfica, podemos ver quais valores de correspondem aos achados acima.
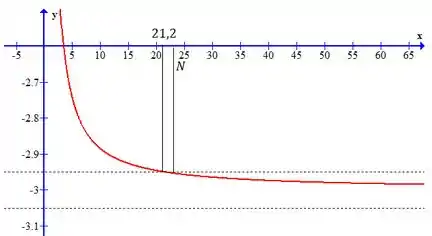
Para .
Então, podemos estabelecer um número imediatamente maior:
Deste modo que, para qualquer:
E aí! o que achou? Responde Aí!