Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.3 - Ex. 5
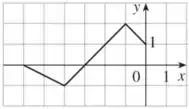
O gráfico de é dado. Esboce os gráficos das seguintes funções:
Passo 1
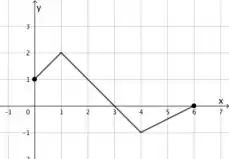
Eaee, belezinha?? Bom... A questão nos dá o seguinte gráfico de uma função :
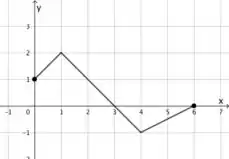
E ela quer que, a partir desse gráfico, esbocemos os seguintes:
Para isso, ao comparar com , temos que analisar o que acontece com esses sinais e números colocados que tornam as funções diferentes.
E aí?? Bora lá?? 😉
Passo 2
Vamos começar com a letra a) .
A transformação que faremos no gráfico de é multiplicar por e ficar com .
O que isso vai mudar no meu gráfico inicial?
Bom, quando multiplicamos o por uma constante , a interpretação geométrica é que o gráfico vai ser comprimido horizontalmente por um fator .
Assim, o domínio vai mudar, pois, neste caso, devemos ter (veja que o domínio de é ), e dividindo tudo por , temos o dominio de
Assim, o gráfico será:
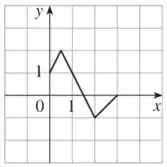
Observe que agora o ponto de corresponde ao ponto em .
Passo 3
Na letra b), temos:
Agora, a transformação que faremos no gráfico de é multiplicar por e ficar com . O que isso vai mudar no meu gráfico inicial?
Quando multiplicamos o por uma constante , a interpretação geométrica é que o gráfico vai ser esticado horizontalmente por um fator 2. Assim, o domínio vai mudar, pois, neste caso, devemos ter (o domínio de é ), e multiplicando tudo por , temos o dominio de
O gráfico será:
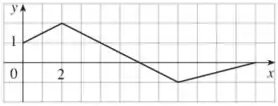
Observe que agora o ponto de corresponde ao ponto em .
Passo 4
Na letra c), temos:
Agora, a transformação que faremos no gráfico de é multiplicar por e ficar com . O que isso vai mudar no meu gráfico inicial?
Quando multiplicamos o por , a interpretação geométrica é que o gráfico vai refletido em torno do eixo . Assim, o domínio vai mudar, pois, neste caso, devemos ter (o domínio de é ), e multiplicando tudo por , temos o dominio de
O gráfico será:
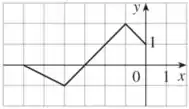
Observe que agora o ponto de corresponde ao ponto em .
Passo 5
Na letra d), temos:
Agora, a transformação que faremos no gráfico de , gráfico da letra c), é multiplicar por e ficar com . O que isso vai mudar no meu gráfico inicial?
Nesse caso, todos os valores de estão sendo multiplicados por , ou seja, todos os pontos vão ser refletidos em torno do eixo . O domínio vai continuar sendo o domínio de .
O gráfico será:
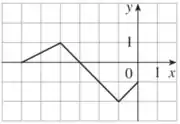
Observe que agora o ponto de corresponde ao ponto em .
Resposta
a)
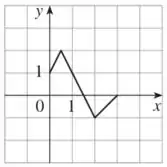
b)
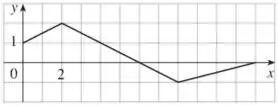
c)
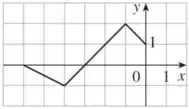
d)
