Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 55
Localize os arcos . Em seguida, dê o sinal do cosseno de cada um deles.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro vamos localizar os arcos no ciclo trigonométrico.
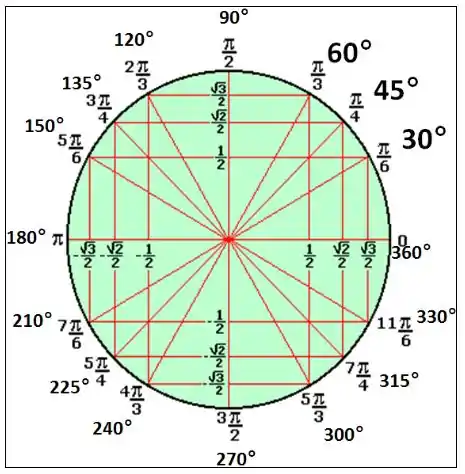
Ou seja, temos um valor em cada quadrante.
Passo 2
Agora, vamos ver os sinais da função cosseno.
Sabemos que a função cosseno é positiva no primeiro e quarto quadrante, e negativa nos outros dois. Desse modo, os sinais são, em ordem:
Resposta
Vide passo a passo
Exercícios de Livros Relacionados
Localize os arcos no ciclo trigonométrico e coloque em ordem crescente os números c o t g60 ° ,c o t g1 2 0 ° ,c o t g2 1 0 °ec o t g330 ° .
Localize os arcos no ciclo trigonométrico e coloque em ordem crescente os números t g60 ° ,t g1 2 0 ° ,t g2 1 0 °et g330 ° .
Localize os arcos no ciclo trigonométrico e coloque em ordem crescente os números c o s s e c60 ° ,c o s s e c150 ° ,c o s s e c240 °ec o s s e c3 0 0 ° .
Usando simetria e sabendo que t gπ 6 = 3 3 , dê o valor da tangente de 5 π 6 , 7 π 6e11 π 6 .
Qual é o valor de (c o s s e c (pi)/(6) + s e n (pi)/(6)) (s e n (pi)/(4) - sec (pi)/(3)) ?