Enunciado
Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 4.Exercícios - Ex. 88
Localize os arcos no ciclo trigonométrico e coloque em ordem crescente os números .
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro vamos localizar os arcos no ciclo trigonométrico
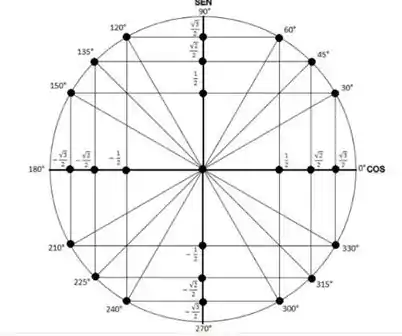
Passo 2
Agora, vamos lembrar que a função cossecante é o inverso da função seno.
Ou seja, segue as mesmas regras de sinais, positiva nos dois primeiros quadrantes e negativa nos dois últimos.
Logo:
E assim:
Resposta
Exercícios de Livros Relacionados
Reduza ao 1° quadrante:a) cos 178 ° b) c o t g7 π 6 c) s e n7 π 6 d) s e n5 π 4 e) s e n251 ° f) sec 124 ° g) cos 5 π 3 h) cos 7 π 6 i) t g290 ° j) c o s s e c11 π 6 k) t g3 π 4 l) t g5 π 3
Reduza ao intervalo 0 , π 4 :a) s e n261 ° b) s e n4 π 3 c) s e n5 π 6 d) s e n5 π 3 e) cos 341 ° f) cos 2 π 3 g) cos 7 π 6 h) cos 4 π 3 i) t g151 ° j) t g5 π 3 k) t g11 π 6 l) t g2 π 3
Represente, no ciclo as imagens dos seguintes conjuntos de números reais: E = x∈ R |x = k π ,k ∈ Z F = x∈ R |x = k π 2 ,k ∈ Z G = x∈ R |x = π 3 + k π ,k ∈ Z H = x∈ R |x = π 4 + k π 2 ,k ∈ Z
Qual é o sinal do cosseno de cada arco abaixo?
Você pode observar no exercício 54 que π 4e7 π 4 são simétricos em relação ao eixo u, assim como 3 π 4e5 π 4 . Sabendo que c o s c o sπ 4 = 2 2 e c o s 3 π 4 = - 2 2 , dê o valor de c o s c o s7 π 4 e