Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 62
62. Max-min. O arco gira em torno da reta , para gerar o sólido da figura a seguir.
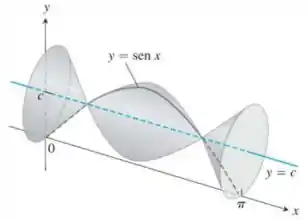
a. Determine o valor de que minimiza o volume do sólido. Qual é o volume mínimo?
b. Que valor de em maximiza o volume do sólido?
c. Desenhe o gráfico do volume do sólido em função de , primeiro para e depois em um domínio maior. O que acontece com o volume do sólido quando se afasta de ? Isso faz sentido fisicamente? Justifique sua resposta.
Passo 1
a) Então pessoal, de ínicio o que precisamos fazer é determinar o volume desse trem aí! Como a revolução ocorre em torno da reta , então chegaremos em uma expressão do volume em função de com cerveja! Para calcularmos o volume disso, basta utilizarmos a expressão que o George nos cede na seção 5.4, se liga:
Mas quem é esse termo ? Esse termo é a função raio do sólido, gente! Como não está na origem como comumente aparece, galera, então nosso raio será o seguinte:
Note que o módulo tem que ser colocado porque não sabemos o valor de e aí colocando o módulo, independentemente do valor que seja, não mudaria em nada nosso cálculo, tudo bem? Sendo assim, nossa integral será:
Aqui vale ressaltar que o módulo some por conta do quadrado e o intervalo de integração é , assim como enfatizado pela figura, ok?!
Passo 2
Agora que temos uma integral bonitinha para ser resolvida, então vamos resolve-la uaaai! Reescrevendo a integral para facilitar nossa vida, teremos:
Para essa segunda integral, qual é a função que derivamos e resulta em ? Sim, a resposta é , não é mesmo? Ademais, o resultado da terceira integral também é tabelado e é esse aqui:
Sendo assim, nosso volume será:
Passo 3
Agora que encontramos uma expressão para o volume, o que devemos fazer é derivar essa função e igualar a zero para descobrirmos os pontos críticos da função e, portanto, o valor de que minimiza o volume do sólido. Fazendo isso, teremos:
Esse ponto é um ponto crítico! Substituindo esse ponto na função original, teremos:
Dessa forma, podemos concluir que o valor de volume que encontramos é o volume mínimo e o valor de que encontramos é o valor que minimiza o volume do sólido.
Passo 4
b) Para descobrirmos isso, vamos escrever o volume para os dois pontos extremos dado pela questão, que são e , se liga:
Os resultados nos levam a concluir que maximiza o volume do sólido, uma vez que é o máximo absoluto da função.
Passo 5
c) Se plotarmos o gráfico da função , teremos o seguinte:
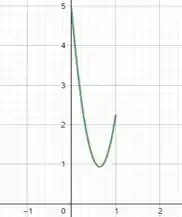
Quando esse gráfico é extendido para intervalos maiores que , o que notamos é uma explosão de volume! Esse tipo de coisa não é explicado fisicamente, até porque o próprio gráfico é um gráfico complexo. Sendo assim, a conclusão é que não faz sentido fisicamente.
Resposta
a)
b)
c) Não faz sentido fisicamente.