Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 57

Uma molécula de metano, C H 4 , é estruturada com os quatro átomos de hidrogênio nos vérticies de um tetraedro regular e o carbono no centro. O ângulo de vínculo é o ângulo formado pela ligação H - C - H : é o ângulo entre as retas que ligam o carbono a dois átomos de hidrogênio. Mostre que esse ângulo de vinculo é de aproximadamente 109,5 ° .

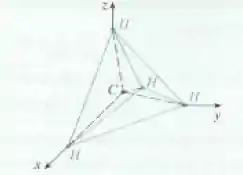
[Sugestão: tome os verticies do tetraedro em 1,0 , 0 ,   0,1 , 0 ,   ( 0,0 , 1 ) e ( 1,1 , 1 ) , como exposto na figura. Mostre então que o centro é 1 2 , 1 2 , 1 2 ].

Passo 1

Vamos considerar os hidrogênios que estão no eixo x e no eixo y , ou seja, os hidrogênios que estão nos pontos

( 1,0 , 0 )

E

( 0,1 , 0 )

Estando o carbono no centro 1 2 , 1 2 , 1 2 , os vetores que ligam o carbono até cada um desses átomos de hidrogênio são:

d = 1,0 , 0 - 1 2 , 1 2 , 1 2 = 1 2 , - 1 2 , - 1 2

E

v = 0,1 , 0 - 1 2 , 1 2 , 1 2 = - 1 2 , 1 2 , - 1 2

Passo 2

Dito isso, o ângulo entre dois vetores pode ser calculado por

c o s θ = d → ∙ v → d v  

Vamos então calcular esse produto escalar do numerador e o modulo dos vetores do denominador:

d → ∙ v → = 1 2 , - 1 2 , - 1 2 ∙ - 1 2 , 1 2 , - 1 2 = 1 2 . - 1 2 - 1 2 ∙ 1 2 - 1 2 ∙ - 1 2 = - 1 4

d = 1 2 2 + - 1 2 2 + - 1 2 2 = 3 4

v = - 1 2 2 + 1 2 2 + - 1 2 2 = 3 4

Passo 3

Substituindo tudo na formula:

c o s θ = 1 2 , - 1 2 , - 1 2 ∙ - 1 2 , 1 2 , - 1 2 d v = - 1 4 3 4 3 4 = - 1 3

Assim,

θ = arccos ⁡ - 1 3 ≈ 109,5 °

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre um vetor unitário que tenha a mesma direção que o vetor dado:
Encontre um vetor unitário que tenha a mesma direção que o vetor dado:
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.
Encontre um vetor a → com representação dada pela direção da linha A B → . Desenhe A B → e a representação equivalente a partir da origem.