Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 12

Mostrar que o volume do maior cilindro reto que pode ser inscrito num cone reto é 4 / 9 do volume do cone.

Passo 1

Inicialmente, vamos fazer um esboço do que está acontecendo, olha só:

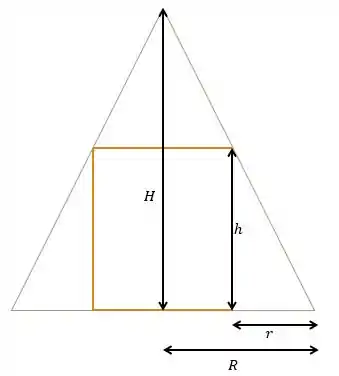
Repare que o triângulo pequeno, é semelhante ao triângulo grande. Assim,

h r = H R

Logo,

h = H r R

Passo 2

Para acharmos o maior cilindro, vamos expressar o volume e maximizar. Vem comigo!

V = A b a s e × h

Logo,

V = π R - r 2 h

Substituindo a expressão de h que encontramos no Passo 1:

V = π R - r 2 H r R

Assim,

V ' r = H π R R - r 2 r

Para maximizar, vamos derivar a expressão de V e igualar a zero. Usando a regra do produto:

V ' r =   H π R 2 R - r × - 1 × r + R - r 2

Igualando a zero:

H π R - 2 r R - r + R - r 2 = 0

Portanto,

R - r 2 = 2 r R - r

Como r ≠ R :

R - r = 2 r → R = 3 r

Passo 3

Agora que já achamos a relação entre os raios, vamos calcular a razão dos volumes.

V c o n e = 1 3 π R 2 H

Para o cilindro:

V c i l i n d r o = π R - r 2 h

Fazendo a razão:

V c i l i n d r o V c o n e = π R - r 2 h 1 3 π R 2 H

Logo,

V c i l i n d r o V c o n e = 3 R - r 2 h R 2 H

Como h = H r R :

V c i l i n d r o V c o n e = 3 R - r 2 H r R R 2 H

Simplificando:

V c i l i n d r o V c o n e = 3 R - r 2 r R 3

Pra finalizar, vamos usar que   R = 3 r :

V c i l i n d r o V c o n e = 3 2 r 2 r 3 r 3

Portanto,

V c i l i n d r o V c o n e = 4 9

Com isso mostramos o que ele nos pede 😉

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça um esboço do gráfico de uma função f que passa pelos pontos c , f c , d , f d , e , f e , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pont
Faça um esboço do gráfico de uma função f que passa pelos pontos c , f c , d , f d , e , f e , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pont
Faça um esboço do gráfico de uma função f que passa pelos pontos c , f c , d , f d , e , f e , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pont
Faça um esboço do gráfico de uma função f que passa pelos pontos c , f c , d , f d , e , f e , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pont
Faça um esboço do gráfico de uma função f que passa pelos pontos c , f c , d , f d , e , f e , se as condições dadas forem satisfeitas. Trace também um segmento da reta tangente em cada um desses pont